在平面直角坐标系xOy中,已知对于任意实数k,直线( k+1)x+(k-
k+1)x+(k- )y-(3k+
)y-(3k+ )=0恒过定点F.设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为2+
)=0恒过定点F.设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为2+ .
.
(1)求椭圆C的方程;
(2)设(m,n)是椭圆C上的任意一点,圆O:x2+y2=r2(r>0)与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
(本小题满分12分)
有4张面值相同的债券,其中有2张中奖债券.
(1)有放回地从债券中任取2次,每次取出1张,计算取出的2张都是中奖债券的概率.
(2)无放回地从债券中任取2次,每次取出1张,计算取出的2张中至少有1张是中奖债券的概率.
(本小题满分14分)(注意:仙中、一中、八中的学生三问全做,其他学校的学生只做前两问)
已知函数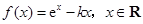
(Ⅰ)若 ,试确定函数
,试确定函数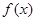 的单调区间;
的单调区间;
(Ⅱ)若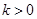 ,且对于任意
,且对于任意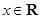 ,
,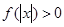 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(Ⅲ)设函数 ,求证:
,求证: .
.
(本小题满分13分)
已知数列{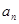 }满足
}满足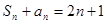 ,
,
(I)写出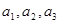 ,并推测
,并推测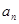 的表达式;
的表达式;
(II)用数学归纳法证明所得的结论。
(本题满分13分) 已知函数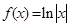
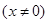 ,函数
,函数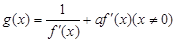
(I)当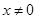 时,求函数
时,求函数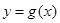 的表达式;
的表达式;
(II)若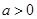 ,且函数
,且函数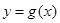 在
在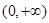 上的最小值是2 ,求
上的最小值是2 ,求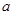 的值;
的值;
(III)对于(II)中所求的a值,若函数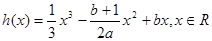 ,恰有三个零点,求b的取值范围。
,恰有三个零点,求b的取值范围。
在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E的棱AB上移动。
(I)证明:D1E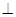 A1D;
A1D;
(II)AE等于何值时,二面角D1-EC-D的大小为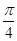 。
。