如图,在三棱锥S ABC中,平面EFGH分别与BC,CA,AS,SB交于点E,F,G,H,且SA⊥平面EFGH,SA⊥AB,EF⊥FG.
求证:(1)AB∥平面EFGH;
(2)GH∥EF;
(3)GH⊥平面SAC.
 (本小题満分14分)
(本小题満分14分)
二次函数f(x+1)-f(x)=2x,且f(0)=1
(1)求f(x)的解析式;
(2)在区间[-1,1]上,y= f(x)的图像恒在y=2x+m的图像上方,试确定实数m的取值范围。
(本小题満分14分)
已知函数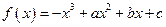 图像上的点
图像上的点 处的切线方程为
处的切线方程为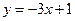 .
.
(1)若函数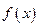 在
在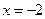 时有极值,求
时有极值,求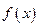 的表达式
的表达式
(2)若函数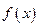 在区间
在区间 上单调递增,求实数
上单调递增,求实数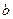 的取值范围
的取值范围
本小题満分14分)
如图,△OAB是边长为2的正三角形,记△OAB位于直线 左侧的图形的面积为
左侧的图形的面积为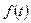 。试求函数
。试求函数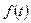 的解析式,并
的解析式,并 画出函数
画出函数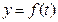 的图象.
的图象.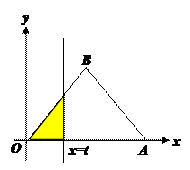
(本小题15分)
如图在三棱锥P-ABC中,PA
 分别在棱
分别在棱 ,
,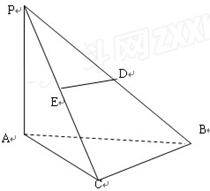
(1)求证:BC
(2)当D为PB中点时,求AD与平面PAC所成的角的余弦值;
(3)是否存在点E,使得二面角A-DE-P为直二面角,并说明理由。
(本小题15分)
已知函数 有极值.
有极值.
(1)求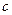 的取值范围;
的取值范围;
(2)若 在
在 处取得极值,且当
处取得极值,且当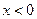 时,
时,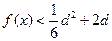 恒成立,求
恒成立,求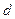 的取值范围.
的取值范围.