如图,设椭圆 :
: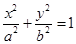
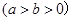 的离心率
的离心率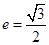 ,顶点
,顶点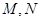 的距离为
的距离为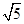 ,
, 为坐标原点.
为坐标原点.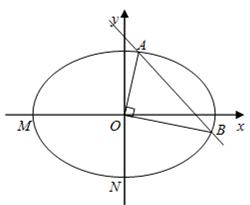
(1)求椭圆 的方程;
的方程;
(2)过点 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆 分别交于
分别交于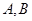 两点.
两点.
(ⅰ)试判断点 到直线
到直线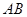 的距离是否为定值.若是请求出这个定值,若不是请说明理由;
的距离是否为定值.若是请求出这个定值,若不是请说明理由;
(ⅱ)求 的最小值.
的最小值.
(本小题满分14分)
如图所示,棱长为2的正方体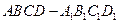 中,
中,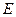 、
、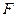 分别为
分别为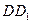 、
、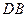 的中点.
的中点.
(Ⅰ)求证: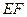 //平面
//平面 ;
;
(Ⅱ)求证: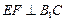 ;
;
(Ⅲ)求三棱锥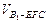 的体积.
的体积.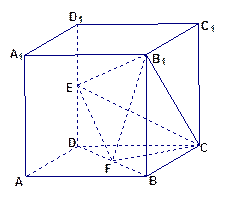
(本小题满分14分)
一个口袋中装有大小相同的二个白球: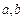 ,三个黑球:
,三个黑球: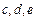 .
.
(Ⅰ)若从口袋中随机地摸出一个球,求恰好是白球的概率;
(Ⅱ)若从口袋中一次随机地摸出两个球,求恰好都是白球的概率.
(本小题满分12分)
设函数f (x)=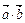 ,其中向量
,其中向量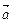 =(
=( cosx+1,
cosx+1,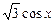 ),
),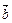 =(
=( cosx-1,2sinx),x∈R.(Ⅰ)求f (x)的解析式;(Ⅱ)求f (x)的最小正周期、对称轴方程和对称中心的坐标。
cosx-1,2sinx),x∈R.(Ⅰ)求f (x)的解析式;(Ⅱ)求f (x)的最小正周期、对称轴方程和对称中心的坐标。
(本小题满分14分)设数列{an}和{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,且数列{an+1-an}是等差数列,数列{bn―2}是等比数列(n∈N*).
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)是否存在k∈N*,使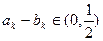 ?若存在,求出k,若不存在,说明理由.
?若存在,求出k,若不存在,说明理由.
(本小题满分14分)已知椭圆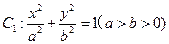 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C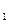 上任一点,MN是圆
上任一点,MN是圆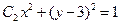 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为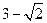 的直线
的直线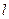 恰好与圆
恰好与圆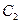 相切.
相切.
(Ⅰ)求椭圆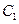 的离心率;
的离心率;
(Ⅱ)若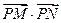 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的方程.
的方程.