如图,在长方体AC1中,AB=BC=2,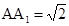 ,点E、F分别是面A1C1、面BC1的中心.
,点E、F分别是面A1C1、面BC1的中心.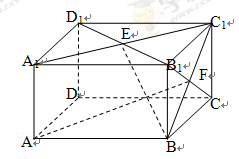
(1)求证:BE//平面D1AC;
(2)求证:AF⊥BE;
(3)求异面直线AF与BD所成角的余弦值。
如图,四棱锥S—ABCD的底面为正方形,SD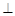 底面ABCD,则下列结论中不正确的是()
底面ABCD,则下列结论中不正确的是()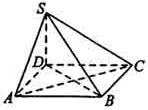
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60), ,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: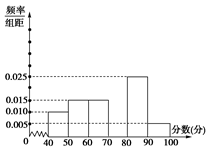
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.
两人约定在20∶00到21∶00之间相见,并且先到者必须等迟到者40分钟方可离去,如果两人出发是各自独立的,在20∶00至21∶00各时刻相见的可能性是相等的,求两人在约定时间内相见的概率。
某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
| 商店名称 |
A |
B |
C |
D |
E E |
| 销售额x(千万元) |
3 |
5 |
6 |
7 |
9 9 |
| 利润额y(千万元) |
2 |
3 |
3 |
4 |
5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性。
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
一个包装箱内有6件产品,其中4件正品,2件次品。现随机抽出两件产品,
(1)求恰好有一件次品的概率。
(2)求都是正品的概率。
(3)求抽到次品的概率