如图所示,在直角梯形ABCD中,∠A=∠B=90°,AD∥BC,E为AB上的点,DE平分∠ADC,CE平分∠BCD,以AB为直径的圆与CD有怎样的位置关系?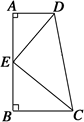
(本小题满分9分)设三角形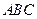 的内角
的内角 的对边分别为
的对边分别为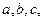
 ,
,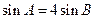 .
.
(1)求 边的长;
边的长;
(2)求角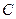 的大小;
的大小;
(3)求三角形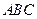 的面积
的面积 。
。
已知二次函数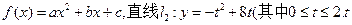
为常数) ;
; .若直线
.若直线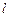 1、
1、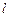 2与函数
2与函数 的图象以及
的图象以及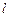 2,y轴与函数
2,y轴与函数 的图象
的图象
所围成的封闭图形如阴影所示.
(1)求
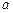 、b、c的值;
、b、c的值;
(2)求阴影面积S关于t的函数S(t)的解析式;
(3)若 问是否存在实数m,使得
问是否存在实数m,使得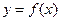 的图象与
的图象与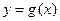 的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
 已知数列
已知数列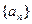 ,其前n项和
,其前n项和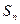 ,满足
,满足 ,且
,且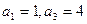
 。
。
(1)求实数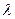 的值;
的值;
(2)求数列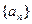 的通项公式
的通项公式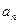 ;
;
(3)设 数列
数列 的前
的前 项和为
项和为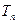 ,试比较
,试比较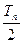 与
与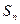 的大小.
的大小.
( 12分)设函数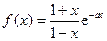 .
.
(1)写出定义域及 的解析式;
的解析式;
(2)设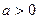 ,讨论函数
,讨论函数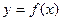 的单调性;
的单调性;
(3)若对任意 ,恒有
,恒有 成立,求实数
成立,求实数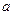 的取值范围.
的取值范围.
已知向量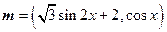 ,
,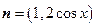 ,设函数
,设函数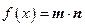 .
.
(1)求 的最小正周期与单调递增区间;
的最小正周期与单调递增区间;
(2)在△ 中,
中,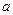 、
、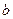 、
、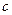 分别是角
分别是角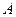 、
、 、
、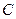 的对边,若
的对边,若 △
△ 的面积为
的面积为 ,求
,求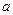 的值.
的值.