已知椭圆C: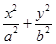 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为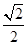 ,一条准线l:x=2.
,一条准线l:x=2.
(1)求椭圆C的方程;
(2)设O为坐标原点,M是l上的点,F为椭圆C的右焦点,过点F作OM的垂线与以OM为直径的圆D交于P,Q两点.
①若PQ=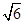 ,求圆D的方程;
,求圆D的方程;
②若M是l上的动点,求证点P在定圆上,并求该定圆的方程.
已知函数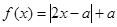 。
。
(1)若不等式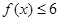 的解集为
的解集为
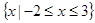 ,求实数
,求实数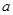 的值;
的值;
(2)在(1)的条件下,若存在实数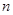 使
使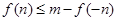 成立,求实数m的取值范围。
成立,求实数m的取值范围。
用总长14.8m的钢条制成一个长方体容器的框架,如果所制做容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积。
已知数列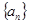 是递增数列,且满足
是递增数列,且满足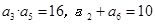 。
。
(1)若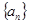 是等差数列,求数列
是等差数列,求数列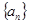 的通项公式;
的通项公式;
(2)对于(1)中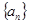 ,令
,令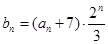 ,求数列
,求数列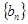 的前
的前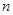 项和
项和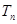 。
。
已知两点A 。
。
(1)求 的对称轴和对称中心;
的对称轴和对称中心;
(2)求 的单调递增区间。
的单调递增区间。
.(本小题满分14分)
已知圆M: 及定点
及定点 ,点P是圆M上的动点,点Q在NP上,点G在MP上,且满足
,点P是圆M上的动点,点Q在NP上,点G在MP上,且满足
(1)求点G的轨迹C的方程;
(2)过点K(2,0)作直线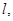 与曲线C交于A、B两点,O是坐标原点,设
与曲线C交于A、B两点,O是坐标原点,设 是否存在这样的直线
是否存在这样的直线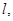 使四边形OASB的对角线相等?若存在,求出直线
使四边形OASB的对角线相等?若存在,求出直线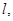 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.