已知圆C1：x2＋y2－2y＝0，圆C2：x2＋(y＋1)2＝4的圆心分别为C1，C2，P为一个动点，且直线PC1，PC2的斜率之积为－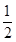
.
(1)求动点P的轨迹M的方程；
(2)是否存在过点A(2，0)的直线l与轨迹M交于不同的两点C，D，使得|C1C|＝|C1D|？若存在，求直线l的方程；若不存在，请说明理由．
本题满分分已知A，B，C，D，E，F是边长为1的正六边形的6个顶点，在顶点取自A，B，C，D，E，F的所有三角形中，随机(等可能)取一个三角形．设随机变量X为取出三角形的面积．
(Ⅰ) 求概率P ( X＝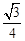
)；
(Ⅱ) 求数学期望E ( X )．
本题满分分已知函数f (x)＝3 sin2 ax＋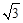
sin ax cos ax＋2 cos2 ax的周期为π，其中a＞0．
(Ⅰ) 求a的值；
(Ⅱ) 求f (x)的值域．
(本小题满分14分)
设椭圆
（
）的两个焦点是
和
（
），且椭圆
与圆
有公共点．
（1）求
的取值范围；
（2）若椭圆上的点到焦点的最短距离为
，求椭圆的方程；
（3）对（2）中的椭圆，直线
（
）与交于不同的两点
、
，若线段
的垂直平分线恒过点
，求实数
的取值范围．
(本小题满分13分)
已知
的展开式前三项中的
的系数成等差数列．
（1）求展开式里所有的的有理项；
（2）求展开式里系数最大的项．
（本小题满分12分）
如图，A，B，C三个观察哨，A在B的正南，两地相距6km，C在B的北偏东60°，两地相距4km.在某一时刻，A观察哨发现某种信号，并知道该信号的传播速度为1km/s；4秒后B,C两个观察哨同时发现这种信号．在以过A,B两点的直线为y轴，以线段AB的垂直平分线为x轴的平面直角坐标系中，试求出发了这种信号的地点P的坐标．