如图所示,在矩形ABCD中,AB=3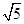 ,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=
,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=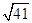 .
.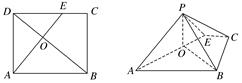
(1)求证:PO⊥平面ABCE;
(2)求二面角EAPB的余弦值.
(本小题满分12分)设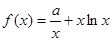 ,
,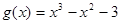 .
.
(1)当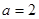 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)如果存在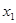 ,
, ,使得
,使得 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数 ;
;
(3)当 时,证明对于任意的
时,证明对于任意的 ,
,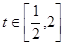 都有
都有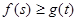 成立.
成立.
(本小题满分12分)
已知椭圆 过点
过点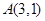 ,左、右焦点分别为
,左、右焦点分别为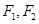 ,离心率为
,离心率为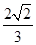 ,经过
,经过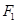 的直线
的直线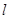 与圆心在
与圆心在 轴上且经过点
轴上且经过点 的圆
的圆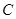 恰好相切于点
恰好相切于点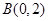 .
.
(1)求椭圆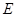 及圆
及圆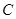 的方程;
的方程;
(2) 在直线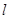 上是否存在一点
上是否存在一点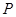 ,使
,使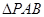 为以
为以 为底边的等腰三角形?若存在,求点
为底边的等腰三角形?若存在,求点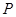 的坐标,否则说明理由.
的坐标,否则说明理由.
(本小题满分12分)在数列 中,
中,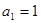 ,
, 为常数,
为常数, ,且
,且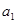 ,
, ,
, 成公比不为1的等比数列.
成公比不为1的等比数列.
(1)求 的值;
的值;
(2)设数列 的前
的前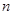 项和为
项和为 ,试比较
,试比较 与
与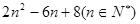 的大小,并说明理由.
的大小,并说明理由.
(本小题满分12分)已知矩形ABCD的边长 ,一块三角板
,一块三角板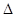 PBD的边
PBD的边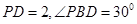 ,且
,且 ,如图.
,如图.
(1)要使三角板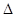 PBD能与平面ABCD垂直放置,求
PBD能与平面ABCD垂直放置,求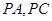 的长;
的长;
(2)求四棱锥 的体积
的体积
(本小题满分12分)已知函数 .
.
(1)若把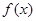 图象上各点的横坐标伸长到原来的2倍,纵坐标不变,再把所得图象向右平移
图象上各点的横坐标伸长到原来的2倍,纵坐标不变,再把所得图象向右平移 ,得到函数
,得到函数 的图象,写出
的图象,写出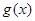 的函数解析式;
的函数解析式;
(2)若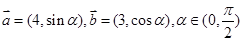 且
且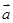 与
与 共线,求
共线,求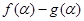 的值.
的值.