如图,在直角坐标系中,已知△PAB的周长为8,且点A,B的坐标分别为(-1,0),(1,0).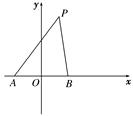
(1)试求顶点P的轨迹C1的方程;
(2)若动点C(x1,y1)在轨迹C1上,试求动点Q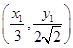 的轨迹C2的方程.
的轨迹C2的方程.
已知函数 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)在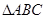 中,
中,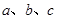 分别是角
分别是角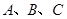 的对边,且
的对边,且 ,求
,求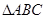 的面积.
的面积.
设函数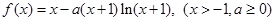 .
.
(1)求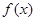 的单调区间;
的单调区间;
(2)当 时,若方程
时,若方程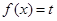 在
在 上有两个实数解,求实数
上有两个实数解,求实数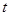 的取值范围;
的取值范围;
(3)证明:当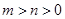 时,
时, .
.
已知椭圆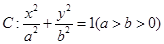 的短半轴长为
的短半轴长为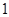 ,动点
,动点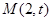
 在直线
在直线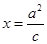 (
(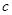 为半焦距)上.
为半焦距)上.
(1)求椭圆的标准方程;
(2)求以 为直径且被直线
为直径且被直线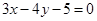 截得的弦长为
截得的弦长为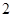 的圆的方程;
的圆的方程;
(3)设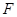 是椭圆的右焦点,过点
是椭圆的右焦点,过点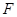 作
作 的垂线与以
的垂线与以 为直径的圆交于点
为直径的圆交于点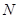 ,
,
求证:线段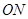 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.
一个口袋中有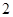 个白球和
个白球和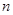 个红球(
个红球(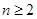 ,且
,且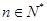 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含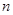 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率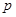 ;
;
(2)若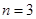 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为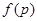 ,当
,当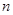 为何值时,
为何值时,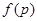 取最大值.
取最大值.
如图,三棱柱 中,侧棱
中,侧棱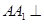 平面
平面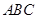 ,
,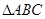 为等腰直角三角形,
为等腰直角三角形,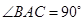 ,且
,且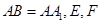 分别是
分别是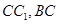 的中点.
的中点.
(1)求证: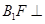 平面
平面 ;
;
(2)求锐二面角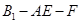 的余弦值.
的余弦值.