已知顶点为原点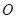 的抛物线
的抛物线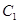 的焦点
的焦点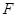 与椭圆
与椭圆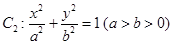 的右焦点重合
的右焦点重合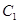 与
与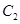 在第一和第四象限的交点分别为
在第一和第四象限的交点分别为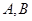 .
.
(1)若△AOB是边长为 的正三角形,求抛物线
的正三角形,求抛物线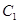 的方程;
的方程;
(2)若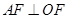 ,求椭圆
,求椭圆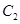 的离心率
的离心率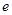 ;
;
(3)点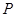 为椭圆
为椭圆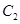 上的任一点,若直线
上的任一点,若直线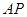 、
、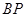 分别与
分别与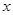 轴交于点
轴交于点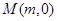 和
和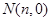 ,证明:
,证明: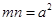 .
.
已知函数
(1)求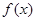 的最小正周期和最大值;
的最小正周期和最大值;
(2)已知 ,求
,求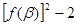 的值.
的值.
下表给出了X、Y、Z三种食物的维生素含量及成本:
| 维生素A (单位\kg) |
维生素B (单位\kg) |
成本 (元\kg) |
|
| X |
300 |
700 |
5 |
| Y |
500 |
100 |
4 |
| Z |
300 |
300 |
2 |
某人欲将这三种食物混合成100kg的食品,要使混合食品中至少含35000单位的维生素A及40000单位的维生素B,那么X、Y、Z这三种食物各取多少kg时,才能使成本最低?最低成本是多少元?
设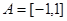 ,
, ,函数
,函数 ,
,
(1)设不等式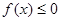 的解集为C,当
的解集为C,当 时,求实数
时,求实数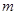 取值范围;
取值范围;
(2)若对任意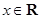 ,都有
,都有 成立,试求
成立,试求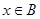 时,
时,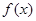 的值域;
的值域;
(3)设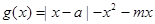
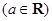 ,求
,求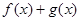 的最小值.
的最小值.
已知集合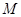 是满足下列性质函数的
是满足下列性质函数的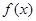 的全体,在定义域
的全体,在定义域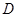 内存在
内存在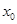 ,使得
,使得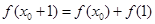 成立。(1)函数
成立。(1)函数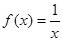 ,
,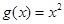 是否属于集合
是否属于集合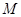 ?分别说明理由。(2)若函数
?分别说明理由。(2)若函数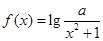 属于集合
属于集合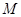 ,求实数
,求实数 的取值范围。
的取值范围。
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为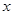 (0<
(0<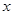 <1
<1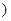 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7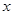 ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.4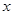 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例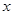 应在什么范围内?
应在什么范围内?
(2)在(1)的条件下,当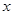 为何值时,本年度的年利润最大?最大利润为多少?
为何值时,本年度的年利润最大?最大利润为多少?