设集合A为函数y=ln(-x2-2x+8)的定义域,集合B为函数y=x+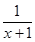 的值域,集合C为不等式
的值域,集合C为不等式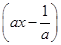 (x+4)≤0的解集.
(x+4)≤0的解集.
(1)求A∩B;
(2)若C⊆∁RA,求a的取值范围.
(本小题满分13分)函数 (
(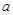 为常数)的图象过点
为常数)的图象过点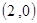 .
.
(1)求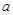 的值;
的值;
(2)函数 在区间
在区间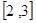 上有意义,求实数
上有意义,求实数 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程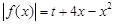 (
(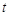 为常数)的正根的个数.
为常数)的正根的个数.
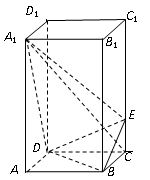
(本小题满分12分)正四棱柱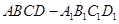 中,
中,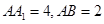 ,点
,点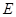 在
在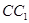 上,且
上,且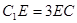 .
.
(1)证明: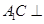 平面
平面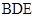 ;
;
(2)求二面角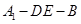 的余弦值.
的余弦值.
(本小题满分12分)已知函数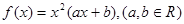 在
在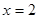 时有极值,其图象在点
时有极值,其图象在点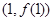 处的切线与直线
处的切线与直线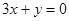 平行.
平行.
(1)求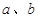 的值和函数
的值和函数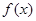 的单调区间;
的单调区间;
(2)若当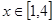 时,恒有
时,恒有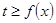 ,试确定
,试确定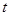 的取值范围.
的取值范围.
(本小题满分12分)设向量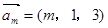 ,
,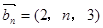 ,其中
,其中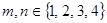 .
.
(1)请列出有序数组 的所有可能结果;
的所有可能结果;
(2)记“使得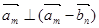 成立的
成立的 ”为事件
”为事件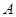 ,求事件
,求事件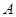 发生的概率.
发生的概率.
(本小题满分12分)如图,直三棱柱 ,底面
,底面 中,
中, ,
, ,棱
,棱 ,
, 分别是
分别是 的中点.
的中点.
(1)求证: ;
;
(2)求直线 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.