在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图:
规定:当产品中的此种元素含量 毫克时为优质品.
毫克时为优质品.
(1)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(2)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数 的分布列及数学期望
的分布列及数学期望 .
.
已知函数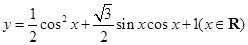 ,求:
,求:
(1)函数的最小正周期;(2)函数的最大值及对应自变量 的集合。
的集合。
设计算法框图,要求输入自变量 的值,输出函数
的值,输出函数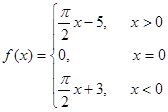 的值。
的值。
两台机床同时生产直径为10的零件,为了检验产品质量,质量质检员从两台机床的产品中各抽取4件进行测量,结果如下:
| 机床甲 |
10 |
9.8 |
10 |
10.2 |
| 机床乙 |
10.1 |
10 |
9.9 |
10 |
如果你是质量检测员,在收集到上述数据后,你将通过怎样的运算来判断哪台机床生产的零件质量更符合要求.
在某中学举行的数学知识竞赛中,将三个年级参赛学生的成绩在进行整理后分成
5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、
第五小组。已知第三小组的频数是15。
(1)求成绩在50—70分的频率是多少;
(2)求这三个年级参赛学生的总人数是多少;
(3)求成绩在80—100分的学生人数是多少;
已知向量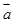 ,
,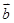 的夹角为
的夹角为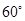 , 且
, 且 ,
,  , 若
, 若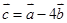 ,
, 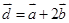 求: (1)
求: (1) 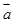 ·
·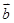 ; (2)
; (2)  .
.