在某中学举行的数学知识竞赛中，将三个年级参赛学生的成绩在进行整理后分成
5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、
第五小组。已知第三小组的频数是15。
（1）求成绩在50—70分的频率是多少；
（2）求这三个年级参赛学生的总人数是多少；
（3）求成绩在80—100分的学生人数是多少； 
某家具城进行促销活动，促销方案是：顾客每消费1000元，便可以获得奖券一张，每张奖券中奖的概率为
，若中奖，则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌，得到3张奖券.
（I）求家具城恰好返还该顾客现金200元的概率；
（II）（文科）求家具城至少返还该顾客现金200元的概率．
（理科）设该顾客有
张奖券中奖，求的分布列，并求的数学
期望E．
在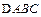
中，a、b、c分别为角A、B、C的对边，且满足
（I）求角
大小；
（II）若
，当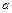
取最小值时，求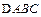的面积.
已知函数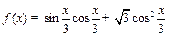
.
（I）将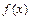
写成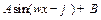
的形式，并求其图象对称中心的横坐标；
（II）如果△ABC的三边a、b、c满足b2= a c，且边b所对的角为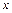
，试求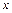的范围及此时函数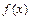的值域.
如图，四棱锥P－ABCD的底面是矩形，侧面PAD
是正三角形，且侧面PAD⊥底面ABCD，E为侧棱PD的中点．
（I）试判断直线PB与平面EAC的关系
（文科不必证明，理科必须证明）；
（II）求证：AE⊥平面PCD；
（III）若AD＝AB，试求二面角A－PC－D
的正切值.
（本小题满分12分）已知数列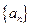
满足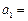
，
（
，
），
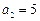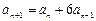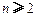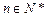若数列
是等比数列.（1）求数列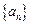
的通项公式；（2）求证：当
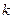为奇数时，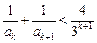
；（3）求证：
（）.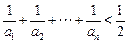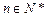