已知二次函数f(x)=px2+qx(p≠0),其导函数为f'(x)=6x-2,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式.
(2)若cn= (an+2),2b1+22b2+23b3+…+2nbn=cn,求数列{bn}的通项公式.
(an+2),2b1+22b2+23b3+…+2nbn=cn,求数列{bn}的通项公式.
(12分) 已知关于 的一元二次不等式
的一元二次不等式 对任意实数
对任意实数 都成立,试比较实数
都成立,试比较实数 的大小.
的大小.
要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18 000 cm2,四周空白的宽度为10 cm,两栏之间的中缝空白的宽度为5 cm,怎样确定广告的高与宽的尺寸(单位cm),能使矩形广告面积最小?
已知等差数列{ }中
}中 .
.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
设正项等差数列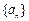 的前n项和为
的前n项和为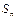 ,其中
,其中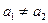 .
. 是数列
是数列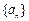 中满足
中满足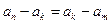 的任意项.
的任意项.
(1)求证: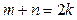 ;
;
(2)若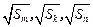 也成等差数列,且
也成等差数列,且 ,求数列
,求数列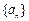 的通项公式;
的通项公式;
(3)求证: .
.
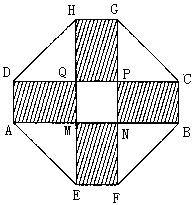
 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形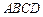 和
和 构成的面积为200
构成的面积为200 的十字型地域,计划在正方形
的十字型地域,计划在正方形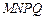 上建一座“观景花坛”,造价为4200元
上建一座“观景花坛”,造价为4200元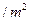 ,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元
,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元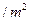 ,再在四个空角(如
,再在四个空角(如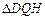 等)上铺草坪,造价为80元
等)上铺草坪,造价为80元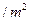 .设
.设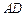 长为
长为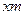 ,
, 长为
长为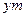 .
.
(1)试找出 与
与 满足的等量关系式;
满足的等量关系式;
(2)设总造价为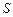 元,试建立
元,试建立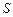 与
与 的函数关系;
的函数关系;
(3)若总造价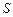 不超过138000元,求
不超过138000元,求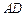 长
长 的取值范围.
的取值范围.