已知在递增等差数列{an}中,a1=2,a1,a3,a7成等比数列,{bn}的前n项和为Sn,且Sn=2n+1-2.
(1)求数列{an}、{bn}的通项公式;
(2)设cn=abn,求数列{cn}的前n项和Tn.
5位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有()
| A.10种 | B.20种 | C.25种 | D.32种 |
三边长均为整数,且最大边长为11,则这样的三角形有多少个?
电视台在“欢乐大本营”节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙信箱中有20封,现由主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有多少种不同的结果?
用n种不同颜色粉笔写黑板报,版块设计如下图1-1-4所示,要求相邻区域不能用同一种颜色的粉笔
(1)当n=6时,板报甲有多少种书写方案?
(2)若板报乙有180种书写方案,求n.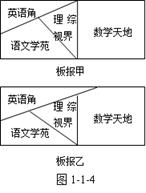
从0,1,2,3,4,5,6中任意取出三个不同的数字作为二次函数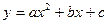 的系数,可有多少个不同的二次函数的表达式?其中二次函数对应的曲线关于y轴对称的有多少个?
的系数,可有多少个不同的二次函数的表达式?其中二次函数对应的曲线关于y轴对称的有多少个?