在直角坐标系 中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C1
中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C1
的极坐标方程为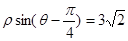 ,曲线C2的直角坐标方程为
,曲线C2的直角坐标方程为 .
.
(1)求曲线C1的直角坐标方程;
(2)已知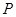 为曲线C2上一点,Q为曲线C1上一点,求P、Q两点间距离的最小值.
为曲线C2上一点,Q为曲线C1上一点,求P、Q两点间距离的最小值.
如图,在直三棱柱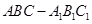 中,
中,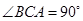 ,
,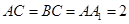 ,
,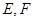 分别是
分别是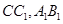 的中点。
的中点。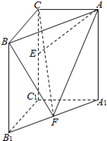
(1)求证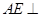 平面
平面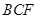 ;
;
(2)求点F到平面ABE的距离。
如图,三棱锥P-ABC中,PA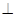 平面ABC,
平面ABC,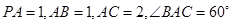 .
.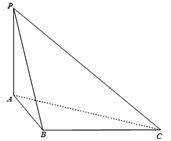
(Ⅰ)求三棱锥P-ABC的体积;
(Ⅱ)证明:在线段PC上存在点M,使得AC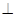 BM,并求
BM,并求 的值.
的值.
如图1,在直角梯形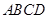 中,
中,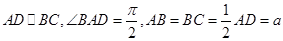 ,
,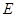 是
是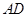 的中点,
的中点, 是AC与
是AC与 的交点,将
的交点,将 沿
沿 折起到图2中
折起到图2中 的位置,得到四棱锥
的位置,得到四棱锥 .
.

(Ⅰ)证明: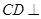 平面
平面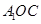 ;
;
(Ⅱ)当平面 平面
平面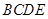 时,四棱锥
时,四棱锥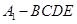 的体积为
的体积为 ,求
,求 的值.
的值.
如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.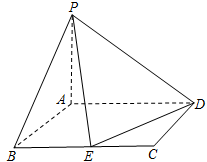
(1)证明:PE⊥DE;
(2)如果PA=2,求异面直线AE与PD所成的角的大小.
如图,在四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(1)证明:EF∥平面PAD;
(2)求三棱锥EABC的体积V.