某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值.
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是矩形,已知AB = 3,AD = 2,PA = 2,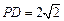 ,
, .
.
(1)证明:AD⊥平面PAB;
(2)求异面直线PC与AD所成的角的大小;
(3)求二面角P—BD—A的大小.
(本小题满分13分)
已知函数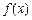 的导数
的导数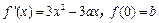 .a,b为实数,
.a,b为实数, .
.
(1)若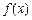 在区间
在区间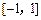 上的最小值、最大值分别为
上的最小值、最大值分别为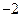 、1,求a、b的值;
、1,求a、b的值;
(2)在 (1) 的条件下,求曲线在点P(2,1)处的切线方程;
(3)设函数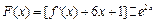 ,试判断函数
,试判断函数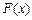 的极值点个数.
的极值点个数.
(本小题满分13分)
某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从2种服装商品,2种家电商品,3种日用商品中,选出3种商品进行促销活动.
(1)试求选出的3种商品中至少有一种是日用商品的概率;
(2)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高150元,同时,若顾客购买该商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得数额为 的奖金.假设顾客每次抽奖时获奖与否的概率都是
的奖金.假设顾客每次抽奖时获奖与否的概率都是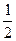 ,请问:商场应将每次中奖奖金数额
,请问:商场应将每次中奖奖金数额 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
(本小题满分13分)
已知函数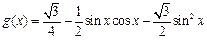 的图象按向量
的图象按向量 平移得到函数
平移得到函数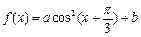 的图象.
的图象.
(1)求实数a、b的值;
(2)设函数 ,求函数
,求函数 的单调递增区间和最值.
的单调递增区间和最值.
(本小题满分12分)设 上的两点,已知向量
上的两点,已知向量 ,
, ,若
,若 且椭圆的
且椭圆的 离心率
离心率 短轴长为
短轴长为 ,
, 为坐标原点.
为坐标原点.
(1)求椭圆的方程;
(2)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.