某高校组织自主招生考试,共有2 000名优秀同学参加笔试,成绩均介于195分到275分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成8组:第1组[195,205),第2组[205,215),…,第8组[265,275].如图是按上述分组方法得到的频率分布直方图,且笔试成绩在260分(含260分)以上的同学进入面试.
(1)估计所有参加笔试的2 000名同学中,参加面试的同学人数;
(2)面试时,每位同学抽取两个问题,若两个问题全答错,则不能取得该校的自主招生资格;若两个问题均回答正确且笔试成绩在270分以上,则获A类资格;其他情况下获B类资格.现已知某中学有两人获得面试资格,且仅有一人笔试成绩为270分以上,在回答两个面试问题时,两人对每一个问题正确回答的概率均为 ,求恰有一名同学获得该高校B类资格的概率.
,求恰有一名同学获得该高校B类资格的概率.
设函数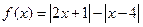 .
.
(I)解不等式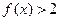 ;(II)求函数
;(II)求函数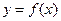 的最小值.
的最小值.
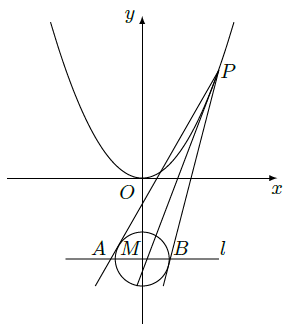
如图,设
是抛物线
:
上动点。圆
:
的圆心为点
,过点
做圆
的两条切线,交直线
:
于
两点。(Ⅰ)求
的圆心
到抛物线
准线的距离。
(Ⅱ)是否存在点
,使线段
被抛物线
在点
处得切线平分,若存在,求出点
的坐标;若不存在,请说明理由.
设函数
(Ⅰ)求 单调区间;
(Ⅱ)求所有实数 ,使 对 恒成立.注: 为自然对数的底数
如图,在三棱锥
中,
,
为
的中点,
平面
,垂足
落在线段
上.
(Ⅰ)证明:
;
(Ⅱ)已知 , , , .求二面角 的大小.


 已知公差不为0的等差数列
的首项
为
(
),且
成等比数列
已知公差不为0的等差数列
的首项
为
(
),且
成等比数列
(Ⅰ)求数列 的通项公式
(Ⅱ)对 ,试比较 与 的大小.