某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数如下表:
| |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲组 |
4 |
5 |
x |
9 |
10 |
| 乙组 |
5 |
6 |
7 |
y |
9 |
(1)已知两组技工在单位时间内加工的合格零件平均数为7,分别求出甲、乙两组技工在单位时间内加工的合格零件的方差,并由此分析两组技工的加工水平;
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工,对其加工的零件进行检测,若2人加工的合格零件个数之和超过14,则称该车间“质量合格”,求该车间“质量合格”的概率.
的内角
所对的边分别为
,向量
与
平行.
(Ⅰ)求
;
(Ⅱ)若
,求
的面积.
已知关于
的不等式
的解集为
.
(Ⅰ)求实数
的值;
(Ⅱ)求
的最大值.
在直角坐标系 中,直线 的参数方程为 ( 为参数).以原点为极点, 轴正半轴为极轴建立极坐标系. 的极坐标方程为 .
(Ⅰ)写出 的直角坐标方程;
(Ⅱ) 为直线 上一动点,当 到圆心 的距离最小时,求 的直角坐标.
如图,
切
于点 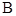 ,直线
交
于
,
,直线
交
于
, 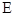 两点,
,垂足为
.
两点,
,垂足为
.
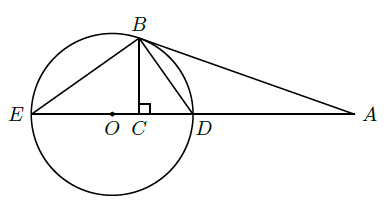
(Ⅰ)证明:
;
(Ⅱ)若
,
,求
的直径.
设
是等比数列 ,
,的各项和,其中
,
,
,的各项和,其中
,
(Ⅰ)证明:函数
在
内有且仅有一个零点(记为
),且
;
(Ⅱ)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为
,比较
与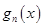 的大小,并加以证明.
的大小,并加以证明.