某城市随机抽取一年（365天）内100天的空气质量指数API的监测数据，结果统计如下：
| API |
 |
 |
 |
 |
 |
 |
 |
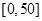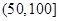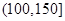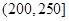| 空气质量 |
优 |
良 |
轻微污染 |
轻度污染 |
中度污染 |
中重度污染 |
重度污染 |
| 天数 |
4 |
13 |
18 |
30 |
9 |
11 |
15 |
（1）若某企业每天由空气污染造成的经济损失S（单位：元）与空气质量指数API（记为w）的关系为：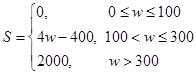
，试估计在本年度内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；
（2）若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染完成下面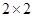
列联表，并判断能否有
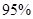的把握认为该市本年空气重度污染与供暖有关？
附：
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| |
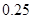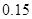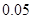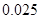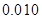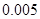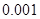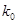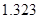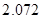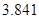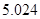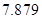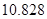非重度污染 |
重度污染 |
合计 |
| 供暖季 |
|
|
|
| 非供暖季 |
|
|
|
| 合计 |
|
|
100 |
厂家在产品出厂前，需对产品做检验，厂家将一批产品发给商家时，商家按合同规定也需随机抽取一定数量的产品做检验，以决定是否接收这批产品．
(1)若厂家库房中的每件产品合格的概率为0.8，从中任意取出4件进行检验，求至少有1件是合格品的概率；
(2)若厂家发给商家20件产品，其中有3件不合格．按合同规定该商家从中任取2件进行检验，只有2件都合格时才接收这批产品，否则拒收．求该商家可能检验出不合格产品数ξ的分布列及数学期望E(ξ)，并求该商家拒收这批产品的概率．
给出四个等式：
1＝1
1－4＝－(1＋2)
1－4＋9＝1＋2＋3
1－4＋9－16＝－(1＋2＋3＋4)
……
（1）写出第5,6个等式，并猜测第n(n∈N*)个等式
（2）用数学归纳法证明你猜测的等式．
打鼾不仅影响别人休息，而且可能与患某种疾病有关．下表是一次调查所得的数据，(1)将本题的2*2联表格补充完整。
(2)用提示的公式计算，每一晚都打鼾与患心脏病有关吗？
提示：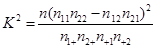
| 患心脏病 |
未患心脏病 |
合计 |
|
| 每一晚都打鼾 |
3 |
17 |
a = |
| 不打鼾 |
2 |
128 |
b = |
| 合计 |
c = |
d = |
n = |
如果复数z＝(m2＋m－1)＋(4m2－8m＋3)i (m∈R)的共轭复数对应的点在第一象限，求实数m的取值范围．
已知函数
．
（1）求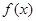
的单调区间；
（2）若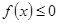
在
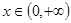上恒成立，求所有实数
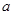的值；
（3）对任意的
，证明：