如图，PA、PB是圆O的两条切线，A、B是切点，C是劣弧AB（不包括端点）上一点，直线PC交圆O于另一点D，Q在弦CD上，且
求证：
（1）
；（2）
∽
泉州市为鼓励企业发展“低碳经济”，真正实现“低消耗、高产出”，施行奖惩制度.通过制定评
分标准，每年对本市
的企业抽查评估，评出优秀、良好、合格和不合格四个等次，
并根据等级给予相应的奖惩（如下表）.某企业投入
万元改造，由于自身技术原因，
能达到以上四个等次的概率分别为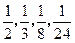
，且由此增加的产值分别为
万元、
万元、
万元、
万元.设该企业当年因改造而增加利润为
.
(Ⅰ)在抽查评估中，该企业能被抽到且被评为合格以上等次的概率是多少？
（Ⅱ）求的数学期望.
| 评估得分 |
 |
 |
 |
 |
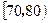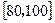| 评定等级 |
不合格 |
合格 |
良好 |
优秀 |
| 奖惩（万元） |
 |
 |
|
|
在棱长为2的正方体ABCD—A1B1C1D1中，E为棱AB的中点，点P在平面A1B1C1D1内，若
D1P⊥平面PCE，试求线段D1P的长。
已知a，b都是正实数，且a+b=2，求证：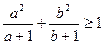
已知函数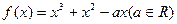
（1）当a=0时，求与直线x-y-10 =0平行，且与曲线y=f(x)相切的直线的方程；
（2）求函数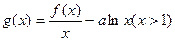
的单调递减区间；
（3）如果存在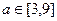
，使函数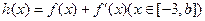
在x=-3处取得最大值，试求b的最大值。
设等比数列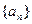
的前n项和为Sn，已知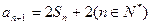
（1）求数列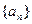通项公式；
（2）在
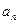与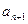
之间插入n个数，使这n+2个数组成一个公差为
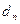的等差数列。
（Ⅰ）求证：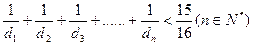
（Ⅱ）在数列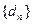
中是否存在三项
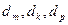（其中m，k，p成等差数列）成等比数列，若存在，求出这样的三项；若不存在，说明理由