设等比数列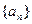 的前n项和为Sn,已知
的前n项和为Sn,已知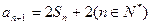
(1)求数列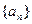 通项公式;
通项公式;
(2)在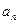 与
与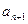 之间插入n个数,使这n+2个数组成一个公差为
之间插入n个数,使这n+2个数组成一个公差为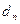 的等差数列。
的等差数列。
(Ⅰ)求证: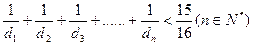
(Ⅱ)在数列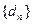 中是否存在三项
中是否存在三项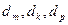 (其中m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由
(其中m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由
已知椭圆的中心在原点,左焦点为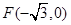 ,右顶点为
,右顶点为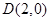 ,设点
,设点 .
.
(1)求该椭圆的标准方程;
(2)若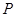 是椭圆上的动点,过P点向椭圆的长轴做垂线,垂足为Q求线段PQ的中点
是椭圆上的动点,过P点向椭圆的长轴做垂线,垂足为Q求线段PQ的中点 的轨迹方程;
的轨迹方程;
.已知 是函数
是函数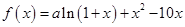 的一个极值点.
的一个极值点.
(1)求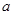 ;
;
(2)求函数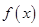 的单调区间.
的单调区间.
从4名书法比赛一等奖的同学和2名绘画比赛一等奖的同学中选出2名志愿者,参加某项服务工作.
(1)求选出的两名志愿者都是获得书法比赛一等奖的同学的概率;
(2)求选出的两名志愿者中一名是获得书法比赛一等奖,另一名是获得绘画比赛一等奖的同学的概率.
对甲、乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下:
| 甲 |
60 |
80 |
70 |
90 |
70 |
| 乙 |
80 |
60 |
70 |
80 |
75 |
问:甲、乙谁的平均成绩最好?谁的各门功课发展较平衡?
已知函数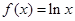 ,
, ,记
,记 .
.
(1)若 ,且
,且 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(2)若 ,且
,且 存在单调递减区间,求
存在单调递减区间,求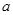 的取值范围;
的取值范围;
(3)若 ,设函数
,设函数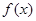 的图象
的图象 与函数
与函数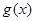 图象
图象 交于点
交于点 、
、 ,过线段
,过线段 的中点作
的中点作 轴的垂线分别交
轴的垂线分别交 ,
, 于点
于点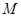 、
、 ,请判断
,请判断 在点
在点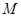 处的切线与
处的切线与 在点
在点 处的
处的 切线能否平行,并说明你的理由.
切线能否平行,并说明你的理由.