已知函数 .
.
(1)求函数 的极值;
的极值;
(2)定义:若函数 在区间
在区间 上的取值范围为
上的取值范围为 ,则称区间
,则称区间 为函数
为函数 的“域同区间”.试问函数
的“域同区间”.试问函数 在
在 上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
(本小题满分12分)
一次考试共有12道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评
分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定
有8道题的答案是正确的,其余题中:有两道题都可判断两个选项是错误的,有一道
题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.请求出该考生:
(1)得60分的概率;
(2)得多少分的可能性最大?
(3)所得分数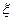 的数学期望(用分数表示,精确到0.01).
的数学期望(用分数表示,精确到0.01).
(本小题满分10分)
已知函数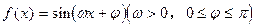 为偶函数,且其图象上相邻两对称轴之间的距离为
为偶函数,且其图象上相邻两对称轴之间的距离为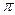 .
.
(I)求函数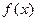 的表达式。
的表达式。
(II)若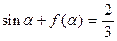 ,求
,求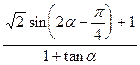 的值.
的值.
已知A(x1,y1),B(x2,y2),写出求直线AB的斜率的一个算法.
写出交换两个大小相同的杯子中的液体(A水、B酒)的算法.
从上海到美国旧金山的海底电缆有15个接点,现在某接点发生故障,需及时修理,为了尽快断定故障发生点,一般至少需要检查几个接点? 