某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩(满分100分，成绩均为不低于40分的整数)分成六段：[40,50)，[50,60)，…，[90,100]后得到如图所示的频率分布直方图．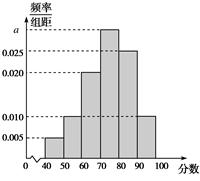
(1)求图中实数a的值；
(2)若该校高一年级共有学生640人，试估计该校高一年级期中考试数学成绩不低于60分的人数；
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生，求这2名学生的数学成绩之差的绝对值不大于10的概率．
已知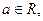
函数
．
（1）当a＝3时，求f（x）的零点；
（2）求函数y＝f (x)在区间[1,2]上的最小值．
设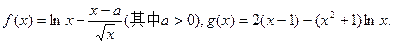
（I）已知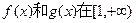
上单调性一致，求a的取值范围；
（II）设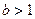
，证明不等式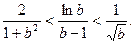
已知函数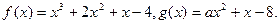
（I）求函数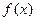
的极值；
（II）若对任意的
的取值范围。
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆，出厂价为13万元/辆，年销售量为5000辆。本年度为适应市场需求，计划提高产品档次，适当增加投入成本，若每辆车投入成本增加的比例为x（0＜x＜1），则出厂价相应提高的比例为0.7x，年销售量也相应增加。已知年利润＝（每辆车的出厂价—每辆车的投入成本）×年销售量。
（I）若年销售量增加的比例为0.4x，为使本年度的年利润比上年度有所增加，则投入成本增加的比例x应在什么范围内？
（II）年销售量关于x的函数为
为何值时，本年度的年利润最大？最大利润为多少？
某市旅游部门开发一种旅游纪念品，每件产品的成本是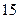
元，销售价是
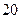元，月平均销售
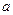件.通过改进工艺，产品的成本不变，质量和技术含金量提高，市场分析的结果表明，如果产品的销售价提高的百分率为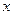
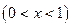，那么月平均销售量减少的百分率为
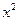.记改进工艺后，旅游部门销售该纪念品的月平均利润是
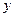（元）.
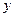(Ⅰ)写出与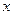的函数关系式；
(Ⅱ)改进工艺后，确定该纪念品的售价，使旅游部门销售该纪念品的月平均利润最大.