如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD= AD,E为CD上一点,且CE=3DE.
AD,E为CD上一点,且CE=3DE.
(1)求证:AE⊥平面SBD.
(2)M,N分别为线段SB,CD上的点,是否存在M,N,使MN⊥CD且MN⊥SB,若存在,确定M,N的位置;若不存在,说明理由.
(本小题满分10分) 选修4—4:坐标系与参数方程.
已知曲线 的参数方程为
的参数方程为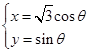 (
(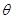 为参数),直线
为参数),直线 的极坐标方程为
的极坐标方程为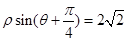 .
.
(1)写出曲线 的普通方程和直线
的普通方程和直线 的直角坐标方程;
的直角坐标方程;
(2)设点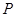 为曲线
为曲线 上的动点,求点
上的动点,求点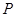 到直线
到直线 距离的最大值.
距离的最大值.
(本小题满分10分) 选修4—1:几何证明选讲.
已知 中,
中,  ,以点
,以点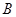 为圆心,以
为圆心,以 为半径的圆分别交
为半径的圆分别交 ,
,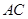 于两
于两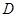 ,
, 两点,且
两点,且 为该圆的直径.
为该圆的直径.
(1)求证:  ;
;
(2)若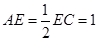 .求
.求 的长.
的长.
(本小题满分12分)
已知函数 .
.
(1)判断函数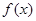 的单调性;
的单调性;
(2)若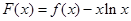 ,若函数
,若函数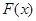 存在零点 ,求实数
存在零点 ,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知椭圆 的方程为
的方程为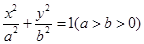 ,离心率
,离心率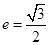 ,过焦点且与长轴垂直的直线被椭圆所截得线段长为1.
,过焦点且与长轴垂直的直线被椭圆所截得线段长为1.
(1)求椭圆 的方程;
的方程;
(2)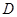 ,
,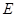 ,
, 为曲线
为曲线 上的三个动点,
上的三个动点, 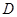 在第一象限,
在第一象限, 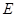 ,
, 关于原点对称,且
关于原点对称,且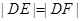 ,问
,问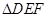 的面积是否存在最小值?若存在,求出此时
的面积是否存在最小值?若存在,求出此时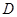 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
(本小题满分12分)
如图,在三棱柱 中,
中, 平面
平面 ,
, ,
,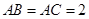 ,
,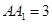 .
.
(1)过 的截面交
的截面交 于
于 点,若
点,若 为等边三角形,求出点
为等边三角形,求出点 的位置;
的位置;
(2)在(1)条件下,求四棱锥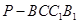 与三棱柱
与三棱柱 的体积比.
的体积比.