某校高三某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下图,据此解答如下问题: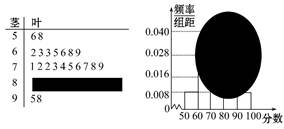
(1)求分数在[50,60)的频率及全班的人数.
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高.
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份在[90,100]之间的概率.
若数列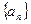 满足前n项之和
满足前n项之和 ,
,
求:(1)bn;
(2) 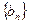 的前n项和Tn。
的前n项和Tn。
已知数列 的首项为
的首项为 =3,通项
=3,通项 与前n项和
与前n项和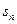 之间满足2
之间满足2 =
=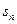 ·
·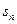
 (n≥2)。
(n≥2)。
(1)求证: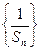 是等差数列,并求公差;
是等差数列,并求公差;
(2)求数列 的通项公式。
的通项公式。
 个正数排成如下表所示的
个正数排成如下表所示的 行
行 列:
列: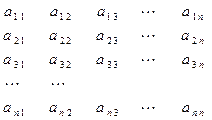
其中每一行成等差数列,每一列成等比数列,且各列的公比相等,若 ,
, ,
,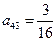 。
。
①求 ;
;
②记 ,求
,求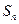 关于
关于 的表达式;
的表达式;
③对于②的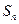 ,求证:
,求证: ;
;
④若集合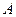 是集合
是集合 的真子集,则称由
的真子集,则称由 的判断到
的判断到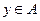 的判断为对
的判断为对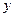 的估计的一次
的估计的一次
优化。请你优化③中的结果。
某地预计从年初开始的前 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量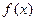 (万件)与月份
(万件)与月份 的近似关系为
的近似关系为 。
。
①写出今年第 个月的需求量
个月的需求量 (万件)与月份
(万件)与月份 的函数关系,并求出哪些个月份的需求量超过1.4万件;
的函数关系,并求出哪些个月份的需求量超过1.4万件;
②如果将该商品每月初都投放市场 万件,要保证每个月都能满足供应,则
万件,要保证每个月都能满足供应,则 至少为多少万件?
至少为多少万件?
若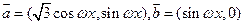 ,其中
,其中 ,记函数
,记函数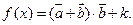
①若 图像中相邻两条对称轴间的距离不小于
图像中相邻两条对称轴间的距离不小于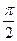 ,求
,求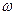 的取值范围;
的取值范围;
②若 的最小正周期为
的最小正周期为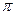 ,且当
,且当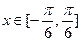 时,
时, 的最大值是
的最大值是 ,求
,求 的解析式,并说明如何由
的解析式,并说明如何由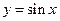 的图像变换得到
的图像变换得到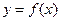 的图像。
的图像。