一个袋中装有若干个大小相同的黑球、白球和红球,已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.
(1)若袋中共有10个球,
①求白球的个数;
②从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
(2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于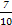 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少.
如图,点 为圆形纸片内不同于圆心
为圆形纸片内不同于圆心 的定点,动点
的定点,动点 在圆周上,将纸片折起,使点
在圆周上,将纸片折起,使点 与点
与点 重合,设折痕
重合,设折痕 交线段
交线段 于点
于点 .现将圆形纸片放在平面直角坐标系
.现将圆形纸片放在平面直角坐标系 中,设圆
中,设圆 :
: ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.
⑴证明曲线 是椭圆,并写出当
是椭圆,并写出当 时该椭圆的标准方程;
时该椭圆的标准方程;
⑵设直线 过点
过点 和椭圆
和椭圆 的上顶点
的上顶点 ,点
,点 关于直线
关于直线 的对称点为点
的对称点为点 ,若椭圆
,若椭圆 的离心率
的离心率 ,求点
,求点 的纵坐标的取值范围.
的纵坐标的取值范围.
某地建一座桥,两端的桥墩已建好,这两墩相距 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,建一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,建一个桥墩的工程费用为256万元,距离为 米的相邻两桥墩之间的桥面工程费用为
米的相邻两桥墩之间的桥面工程费用为 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为 万元。
万元。
(1)试写出 关于
关于 的函数关系式;
的函数关系式;
(2)当 =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使 最小?
最小?
如图,在直三棱柱 中,
中, ,
, 分别是
分别是 的中点,且
的中点,且 .
.
(1)求证: ;
;
(2)求证:平面 平面
平面 .
.
设函数 .
.
(1)求 的最小正周期.
的最小正周期.
(2)若函数 与
与 的图像关于直线
的图像关于直线 对称,求当
对称,求当 时
时 的最大值.
的最大值.
设数列 的前n项和为
的前n项和为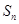 ,
,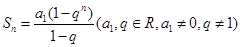
(1)求证:数列 是等比数列;
是等比数列;
(2)若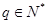 ,是否存在q的某些取值,使数列
,是否存在q的某些取值,使数列 中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由。
中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由。
(3)若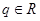 ,是否存在
,是否存在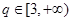 ,使数列
,使数列 中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由。
中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由。