如图，F1、F2分别是椭圆C：
＝1(a＞b＞0)的左、右焦点，A是椭圆C的顶点，B是直线AF2与椭圆C的另一个交点，∠F1AF2＝60°.
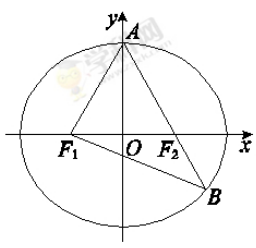
(1)求椭圆C的离心率；
(2)已知△AF1B的面积为40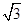
，求a，b的值．
已知等比数列
是递增数列，
，数列
满足
，且
（
）
（1）证明：数列
是等差数列；
（2）若对任意，不等式
总成立，求实数
的最大值．
如图，在三棱锥
中，
，
，
°，平面
平面
，
、
分别为
、
中点．
（1）求证：
；
（2）求二面角
的大小．
如图，已知矩形
所在平面外一点
，
平面，
分别是
的中点，
．
（1）求证：
平面
（2）若
，求直线
与平面
所成角的正弦值．
某商场举行有奖促销活动，顾客购买一定金额商品后即可抽奖，每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中，各随机摸出1个球，在摸出的2个球中，若都是红球，则获一等奖；若只有1个红球，则获二等奖；若没有红球，则不获奖．
（1）求顾客抽奖1次能获奖的概率；
（2）若某顾客有3次抽奖机会，则该顾客在3次抽奖中至多有两次获得一等奖的概率．
某城市
户居民的月平均用电量（单位：度），以
，
，
，
，
，
，
分组的频率分布直方图如图．
（1）求直方图中
的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取
户居民，则月平均用电量在的用户中应抽取多少户？