正项数列{an}的前项和满足: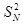 -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.
(1)求数列{an}的通项公式an;
(2)令bn=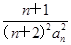 ,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<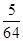 .
.
(本小题8分)每次抛掷一枚骰子(六个面上分别标以数字1,2,3,4,5,6)
(Ⅰ)连续抛掷2次,求向上的数不同的概率
(Ⅱ)连续抛掷2次,求向上的数之和为6的概率
(本小题8分) 已知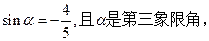
(Ⅰ)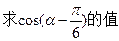
(Ⅱ)求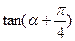 的值.
的值.
(本小题满分14分)
已知函数 ,
, ,且
,且 .
.
(1)试求 所满足的关系式;
所满足的关系式;
(2)若 ,方程
,方程 有唯一解,求
有唯一解,求 的取值范围.
的取值范围.
已知定义  域为
的函数同时满足以下三个条件:
域为
的函数同时满足以下三个条件:
①对任意
,总有
;
②
;
③若  ,则有
成立.
,则有
成立.
(I)求
的值;
(II)判断函数
在区间
上是否同时适合①②③,并给出证明.
(本小题满分12分)
已知函数 .
.
(Ⅰ)当 时,求
时,求 的极小值;
的极小值;
(Ⅱ)若直线 对任意的
对任意的 都不是曲线
都不是曲线 的切线,求
的切线,求 的取值范围.
的取值范围.