求矩阵M=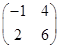 的特征值和特征向量.
的特征值和特征向量.
已知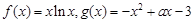 .
.
(1)求函数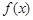 在
在 上的最小值;
上的最小值;
(2)对一切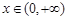 ,
,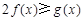 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3) 证明:对一切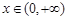 ,都有
,都有 成立.
成立.
设函数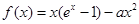
(Ⅰ)若a=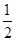 ,求f(x)的单调区间;
,求f(x)的单调区间;
(Ⅱ)若当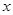 ≥0时f(x)≥0,求a的取值范围。
≥0时f(x)≥0,求a的取值范围。
如图,正方形 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直, ,
,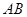 ∥
∥ ,
, ,点
,点 在线段
在线段 上.
上.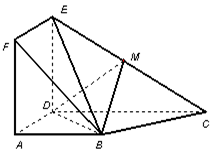
(I)当点 为
为 中点时,求证:
中点时,求证: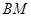 ∥平面
∥平面 ;
;
(II)当平面 与平面
与平面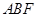 所成锐二面角的余弦值为
所成锐二面角的余弦值为 时,求三棱锥
时,求三棱锥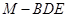 的体积.
的体积.
已知函数 ,其图象过点
,其图象过点
(Ⅰ)求 的值;
的值;
(Ⅱ)将函数 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在
在 上的最大值和最小值。
上的最大值和最小值。
已知数列{ }是等差数列,且满足:a1+a2+a3=6,a5=5;
}是等差数列,且满足:a1+a2+a3=6,a5=5;
数列{ }满足:
}满足: -
-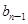 =
= (n≥2,n∈N﹡),b1=1.
(n≥2,n∈N﹡),b1=1.
(Ⅰ)求 和
和 ;
;
(Ⅱ)记数列 =
=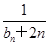 (n∈N﹡),若{
(n∈N﹡),若{ }的前n项和为
}的前n项和为 ,求
,求 .
.