(1)已知两个等比数列{an},{bn},满足a1=a(a>0),b1-a1=1,b2-a2=2,b3-a3=3,若数列{an}唯一,求a的值;
(2)是否存在两个等比数列{an},{bn},使得b1-a1,b2-a2,b3-a3,b4-a4成公差不为0的等差数列?若存在,求{an},{bn}的通项公式;若不存在,说明理由.
(本小题满分12分)设当 时,
时,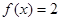 。当
。当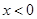 时,
时, ,又
,又 ,写出
,写出 的表达式并作出其图象。
的表达式并作出其图象。
(本小题满分12分)已知函数 是幂函数,且当
是幂函数,且当 时为减函数,
时为减函数,
(1)求实数m的值;
(2)判断函数 奇偶性并说明理由。
奇偶性并说明理由。
(本小题满分12分)已知集合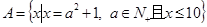 ,
,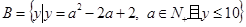 ,求
,求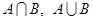 。
。
(本小题满分12分)已知函数 的定义域为
的定义域为 ,且对任意
,且对任意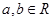 ,都有
,都有 ,当
,当 时,
时, 恒成立.
恒成立.
求证:(1)函数 是奇函数;
是奇函数;
(2)函数 在
在 上是减函数.
上是减函数.
(本小题满分12分)“水”这个曾经被人认为取之不尽、用之不竭的资源,竟然到了严重制约我国经济发展,影响人民生活的程度.因为缺水,每年给我国工业造成的损失达2 000亿元,给我国农业造成的损失达1 500亿元,严重缺水困扰全国三分之二的城市.为了节约用水,某市打算出台一项水费政策,规定每季度每人用水量不超过5吨时,每吨水费1.2元;若超过5吨而不超过6吨时,超过的部分的水费按原价的200%收费;若超过6吨而不超过7吨时,超过部分的水费按原价的400%收费.如果某人本季度实际用水量为x(x≤7)吨,试计算本季度他应交的水费y.(单位:元)