某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
| 产品编号 |
A1 |
A2 |
A3 |
A4 |
A5 |
| 质量指标(x,y,z) |
(1,1,2) |
(2,1,1) |
(2,2,2) |
(1,1,1) |
(1,2,1) |
| |
|
|
|
|
|
| 产品编号 |
A6 |
A7 |
A8 |
A9 |
A10 |
| 质量指标(x,y,z) |
(1,2,2) |
(2,1,1) |
(2,2,1) |
(1,1,1) |
(2,1,2) |
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样本的一等品中,随机抽取2件产品,
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.
我国是水资源匮乏的国家为鼓励节约用水，某市打算出台一项水费政策措施，规定：每一季度每人用水量不超过5吨时，每吨水费收基本价1．3元；若超过5吨而不超过6吨时，超过部分水费加收200%；若超过6吨而不超过7吨时，超过部分的水费加收400%，如果某人本季度实际用水量为
吨，应交水费为
。
（1）求
、
、
的值；
（2）试求出函数的解析式。
已知
是二次函数，且
（1）求的解析式；
（2）求函数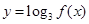
的单调递减区间及值域。
已知
，
（1）证明：
（2）计算
的值
已知集合
（1）求
；（2）求
；（3）若
，求a的取值范围。
已知点
，圆
，过点
的动直线
与圆
交于
两点，线段
的中点为
，O为坐标原点.
（1）求的轨迹方程；
（2）当
时，求的方程及
的面积.