已知圆C：
，圆C关于直线
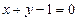对称，圆心在第二象限，半径为
（Ⅰ）求圆C的方程；
（Ⅱ）已知不过原点的直线
与圆C相切，且在x轴、y轴上的截距相等，求直线的方程。
已知函数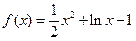
.
（1）求函数
在区间
（
为自然对数的底）上的最大值和最小值；
（2）求证：在区间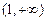
上，函数的图象在函数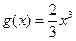
的图象的下方；
（3）求证：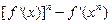
≥
.
已知动圆Q经过点A
,且与直线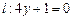
相切，动圆圆心Q的轨迹为曲线C，过定点
作与y轴平行的直线且和曲线C相交于点M1,然后过点M1作C的切线和x轴交于点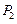
,再过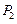作与y轴平行的直线且和C相交于点M2,又过点M2作C的切线和x轴交于点
,如此继续下去直至无穷，记△
的面积为
（Ⅰ）求曲线C的方程；
（Ⅱ）试求
的值。
直线AB过抛物线x2=2py（p>0）的焦点F，并与其相交于A、B两点，Q是线段AB的中点，M是抛物线的准线与y轴的交点，O是坐标原点.
（Ⅰ）求
的取值范围；
（Ⅱ）过A、B两点分别作此抛物线的切线，两切线相交于N点.
求证：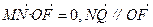
；
（Ⅲ）若p是不为1的正整数，当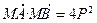
，△ABN的面积的取值范围为［5
，20］时，求该抛物线的方程.
一束光线从点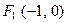
出发，经直线
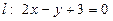上一点
反射后，恰好穿过点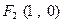
．（Ⅰ）求点
关于直线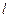
的对称点
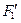的坐标；
（Ⅱ）求以、
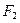为焦点且过点的椭圆
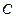的方程；
（Ⅲ）设直线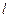与椭圆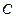的两条准线分别交于
、
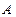两点，点
为线段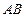
上的动点，求点到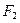的距离与到椭圆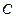右准线的距离之比的最小值，并求取得最小值时点的坐标．
c+bcosC.
,求b的最小值.