某商场销售某种商品的经验表明,该商品每日的销售量y(单
位:千克)与销售价格x(单位:元/千克)满足关系式y=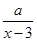 +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
①求a的值;
②若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
在 中,
中, 分别是角
分别是角 的对边,
的对边, 且
且
(1)求 的面积;
的面积;
(2)若 ,求角
,求角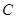 。
。
如图,在棱长为a的正方体ABCD—A1B1C1D1中,M为A1D中点,N为AC中点.
(1)求异面直线MN和AB所成的角;
(2)求证:MN⊥AB1;
(普通班)设函数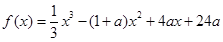 ,其中常数
,其中常数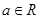 ;(1)讨论
;(1)讨论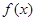 的单调性;(2)若
的单调性;(2)若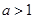 ,当
,当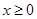 ,
,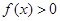 恒成立,求
恒成立,求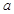 的取值范围。
的取值范围。
(实验班)已知椭圆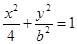 (0<b<2)的离心率等于
(0<b<2)的离心率等于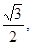 抛物线
抛物线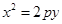 (p>0).
(p>0).
(1)若抛物线的焦点F在椭圆的顶点上,求椭圆和抛物线的方程;
(2)若抛物线的焦点F为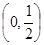 ,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足
,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足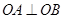 ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
(普通班)已知椭圆 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆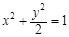 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求k的取值范围.
(实验班)已知函数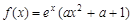
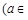 R).
R).
(Ⅰ)若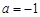 ,求曲线
,求曲线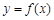 在点
在点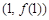 处的的切线方程;
处的的切线方程;
(Ⅱ)若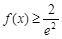 对任意
对任意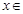
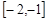 恒成立,求实数
恒成立,求实数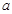 的取值范围.
的取值范围.
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是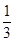 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.