如图所示,机器人海宝按照以下程序运行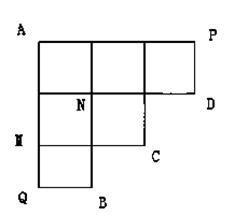
①从A出发到达点B或C或D，到达点B、C、D之一就停止；
②每次只向右或向下按路线运行；
③在每个路口向下的概率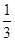
；
④到达P时只向下，到达Q点只向右．
（1）求海宝过点从A经过M到点B的概率，求海宝过点从A经过N到点C的概率；
（2）记海宝到点B、C、D的事件分别记为X=1，X=2，X=3，求随机变量X的分布列及期望．
【改编】如图，在直三棱柱
中，D、E分别为
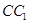、AD的中点，F为
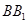上的点，且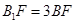
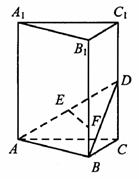
（Ⅰ）证明：EF∥平面ABC；
（Ⅱ）若
，
，
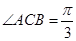（Ⅰ）求三棱锥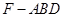
的体积；
（Ⅱ）求二面角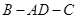
的大小．
在
中，
，
，
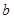分别是角
，
，
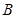的对边，向量
，
，且
//
．
（Ⅰ）求角
的大小；
（Ⅱ）设
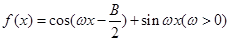，且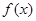
的最小正周期为
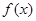，求在区间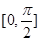
上的最大值和最小值．
【改编】（本小题满分7分）选修4—5：不等式选讲
已知关于
的不等式：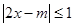
的整数解有且仅有一个值为2．
（Ⅰ）求整数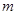
的值；
（Ⅱ）已知a，b，c∈R，若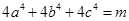
，求
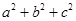的最大值．
（本小题满分7分）《选修4-4：坐标系与参数方程》
已知直线的极坐标方程为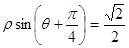
，圆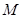
的参数方程为
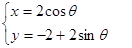（其中
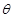为参数）．
（Ⅰ）将直线的极坐标方程化为直角坐标方程；
（Ⅱ）求圆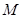上的点到直线的距离的最小值．
的值．