在锐角△ABC中，角A、B、C所对的边长分别为a、b、c.向量m＝(1，cosB)，n＝(sinB，－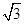
)，且m⊥n.
(1)求角B的大小；
(2)若△ABC面积为10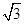，b＝7，求此三角形周长．
在△ABC中，BC＝，AC＝3，sinC＝2sinA.
(1)求AB的值；
(2)求sin的值．
在△ABC中，角A，B，C的对边分别为a，b，c，已知a＋b＝5，c＝，且cos 2C＋2cos(A＋B)＝－.
(1)求角C的大小；
(2)求△ABC的面积S.
设a＝(－1,1)，b＝(4,3)，c＝(5，－2)
(1)求证：a与b不共线，并求a与b的夹角的余弦值；
(2)求c在a方向上的投影；
(3)求λ1和λ2，使c＝λ1a＋λ2b.
已知A(－1,0)，B(0,2)，C(－3,1)，且·＝5，2＝10.
(1)求D点的坐标；
(2)若D的横坐标小于零，试用，表示
已知函数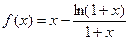
(Ⅰ)求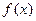
的最小值
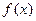（Ⅱ）若在区间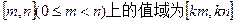
,试求k的取值范围.