(本小题满分12分)已知四棱锥 的底面是边长为2的菱形,且
的底面是边长为2的菱形,且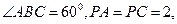
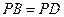 .
.
(Ⅰ)若O是AC与BD的交点,求证: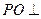 平面
平面 ;
;
(Ⅱ)若点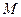 是
是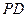 的中点,求异面直线
的中点,求异面直线 与
与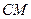 所成角的余弦值.
所成角的余弦值.
已知数列 满足
满足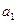 =-1,
=-1, ,数列
,数列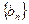 满足
满足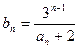
(1)求数列 的通项公式.
的通项公式.
(2)设数列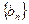 的前
的前 项和为
项和为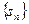 ,求证:当
,求证:当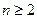 时,
时,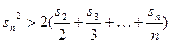 .
.
(3)求证:当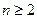 时,
时,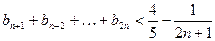
定长为3的线段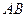 两端点
两端点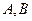 分别在
分别在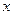 轴,
轴, 轴上滑动,
轴上滑动,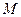 在线段
在线段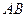 上,且
上,且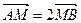
(1)求点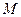 的轨迹
的轨迹 的方程.
的方程.
(2)设过 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线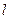 交轨迹
交轨迹 与
与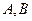 两点.问:线段
两点.问:线段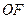 上是否存在一点
上是否存在一点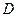 ,使得以
,使得以 为邻边的平行四边形为菱形?作出判断并证明.
为邻边的平行四边形为菱形?作出判断并证明.
已知过点 (1,1)且斜率为
(1,1)且斜率为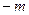 (
( )的直线
)的直线 与
与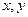 轴分别交于
轴分别交于 两点,分别过
两点,分别过 作直线
作直线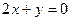 的垂线,垂足分别为
的垂线,垂足分别为 求四边形
求四边形 的面积的最小值.
的面积的最小值.
在 中,点M是BC的中点,
中,点M是BC的中点, 的三边长是连续三个正整数,且
的三边长是连续三个正整数,且
(I)判断 的形状;
的形状;
(II)求 的余弦值。
的余弦值。