某造纸厂拟建一座平面图形为矩形且面积为162m2的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/m2,中间两道隔墙建造单价为248元/m2,池底建造单价为80元/m2,水池所有墙的厚度忽略不计.
(1)试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2)若由于地形限制,该池的长和宽都不能超过16m,试设计污水池的长和宽,使总造价最低,并求出最低总造价.
(本小题满分12分)
已知函数 的最小正周期为
的最小正周期为 ,最小值为
,最小值为 ,图象过点
,图象过点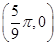 ,(1)求
,(1)求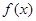 的解析式;(2)求满足
的解析式;(2)求满足 且
且
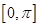 的
的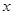 的集合.
的集合.
(本小题满分12分)
已知函数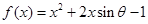 ,
,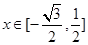
(1)当 时,求
时,求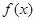 的最大值和最小值
的最大值和最小值
(2)若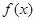 在
在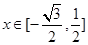 上是单调函数,且
上是单调函数,且 ,求
,求 的取值范围
的取值范围
(本小题满分10分)
如图: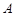 、
、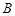 是单位圆
是单位圆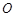 上的点,
上的点,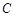 是圆与
是圆与 轴正半轴的交点,三角形
轴正半轴的交点,三角形 为正三角形,且AB∥
为正三角形,且AB∥ 轴.
轴.
(1)求 的三个三角函数值;
的三个三角函数值;
(2)求 及
及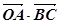 .
.
设数列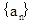 满足:
满足: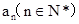 是整数,且
是整数,且 是关于x的方程
是关于x的方程 的根.
的根.
(1)若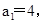 且n≥2时,
且n≥2时,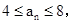 求数列{an}的前100项和S100;
求数列{an}的前100项和S100;
(2)若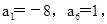 且
且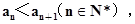 求数列
求数列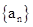 的通项公式.
的通项公式.
已知⊙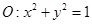 和点
和点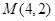 .
.
(Ⅰ)过点 向⊙
向⊙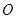 引切线
引切线 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)求以点 为圆心,且被直线
为圆心,且被直线 截得的弦长为4的⊙
截得的弦长为4的⊙ 的方程;
的方程;
(Ⅲ)设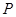 为(Ⅱ)中⊙
为(Ⅱ)中⊙ 上任一点,过点
上任一点,过点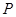 向⊙
向⊙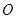 引切线,切点为
引切线,切点为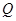 . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点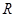 ,使得
,使得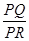 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.