若数列{an}满足an+1=an+an+2(n∈N*),则称数列{an}为“凸数列”.
(1)设数列{an}为“凸数列”,若a1=1,a2=-2,试写出该数列的前6项,并求出前6项之和;
(2)在“凸数列”{an}中,求证:an+3=-an,n∈N*;
(3)设a1=a,a2=b,若数列{an}为“凸数列”,求数列前2011项和S2011.
.(本小题满分12分)如图,在正方体 中,
中, 、
、 分别为棱
分别为棱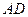 、
、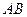 的中点.
的中点.
(1)求证: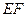 ∥平面
∥平面 ;
;
(2)求证:平面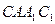 ⊥平面
⊥平面 ;
;
(3)如果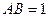 ,一个动点从点
,一个动点从点 出发在正方体的
出发在正方体的
表面上依次经过棱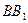 、
、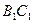 、
、 、
、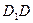 、
、 上的点,最终又回到点
上的点,最终又回到点 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.
.(本小题满分12分)已知函数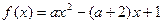 .若
.若 为整数,且函数
为整数,且函数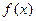 在
在 内恰有一个零点,求
内恰有一个零点,求 的值.
的值.
(本小题满分10分)已知函数 ,
, .
.
(1)求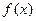 的最大值和最小值;
的最大值和最小值;
(2)若不等式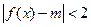 在
在 上恒成立,求实数
上恒成立,求实数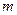 的取值范围.
的取值范围.
.已知 ,函数
,函数 .
.
(1)若函数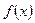 在区间
在区间 内是减函数,求实数
内是减函数,求实数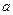 的取值范围;
的取值范围;
(2)求函数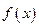 在区间
在区间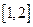 上的最小值
上的最小值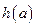 ;
;
(3)对(2)中的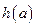 ,若关于
,若关于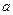 的方程
的方程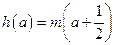 有两个不相等的实数解,
有两个不相等的实数解,
求实数 的取值范围.
的取值范围.
.本小题满分12分)已知函数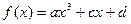
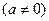 是R上的奇函数,
是R上的奇函数,
当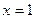 时
时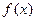 取得极值
取得极值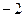 ,
,
(1)求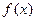 的单调区间和极大值;
的单调区间和极大值;
(2)证明对任意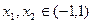 ,不等式
,不等式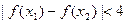 恒成立. 、
恒成立. 、