袋中装有大小相同的黑球和白球共 个,从中任取
个,从中任取 个都是白球的概率为
个都是白球的概率为 .现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取
.现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取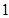 个球,取出的球不放回,直到其中有一人取到白球时终止.用
个球,取出的球不放回,直到其中有一人取到白球时终止.用 表示取球终止时取球的总次数.
表示取球终止时取球的总次数.
(1)求袋中原有白球的个数;
(2)求随机变量 的概率分布及数学期望
的概率分布及数学期望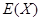 .
.
(本小题满分12分)已知f(x)= 。
。
(1)曲线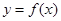 在点(1,f(1))处的切线斜率为0,求f(x)的单调区间;
在点(1,f(1))处的切线斜率为0,求f(x)的单调区间;
(2)若f(x)<x2在(1,+ )恒成立,求a的取值范围。
)恒成立,求a的取值范围。
(本小题满分12分)已知椭圆C: 的离心率为
的离心率为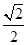 ,连接椭圆四个顶点形成的四边形面积为4
,连接椭圆四个顶点形成的四边形面积为4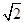 .
.
(1)求椭圆C的标准方程;
(2)过点A(1,0)的直线与椭圆C交于点M, N,设P为椭圆上一点,且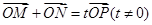 O为坐标原点,当
O为坐标原点,当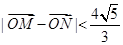 时,求t的取值范围.
时,求t的取值范围.
(本小题满分12分)如图,在三棱锥S -ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC= ,M为AB的中点.
,M为AB的中点.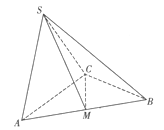
(1)证明:AC⊥SB;
(2)求点B到平面SCM的距离。
(本小题满分12分)某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究.全年级共有1350人,男女生比例为8:7,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为 ,通过对被抽取学生的问卷调查,得到如下2x2列联表:
,通过对被抽取学生的问卷调查,得到如下2x2列联表: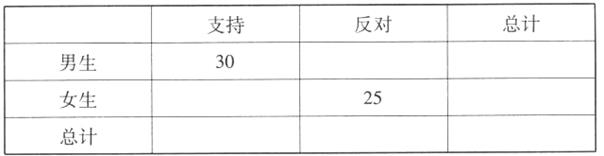
(1)完成列联表,并判断能否有99.9%的把握认为态度与性别有关?
(2)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
(本小题满分12分)已知数列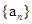 的首项al=1,
的首项al=1,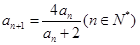 .
.
(1)证明:数列 是等比数列;
是等比数列;
(2)设 ,求数列
,求数列 的前n项和
的前n项和 .
.