已知△ABC的三边长|AB|= ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足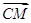 =λ
=λ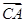 +μ
+μ ,且λμ=
,且λμ= .
.
(1)求|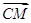 |最小值,并指出此时
|最小值,并指出此时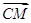 与
与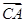 ,
, 的夹角;
的夹角;
(2)是否存在两定点F1,F2使||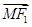 |-|
|-| ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
(本小题满分12分)
有一个容量为50的样本,数据的 分组及各组的频数如下 3;
3; 8;
8; 9;
9; 11;
11; 10;
10; 5;
5; 4.
4.
(1)列频率分布表
(2)画出频率分布直方图
(3)根据频率分布直方图估计数据落在 的概率是多少
的概率是多少
(本小题满分12分)
假 设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间 ,求你离家前不能看到报纸(称事件A)的概率是多少?
设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间 ,求你离家前不能看到报纸(称事件A)的概率是多少?
本小题满分12分)
某 次运动会甲、乙两名射击运动员成绩如下:
次运动会甲、乙两名射击运动员成绩如下:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8. 5,1
5,1 0.1,9.2,10.1,9.1;
0.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;
(2)分别计算两个样本的平均数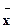 和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。
和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。
(本小题满分12分)
假设有5个条件很类似的女 孩,把她们分别记为A,C,J,K,S。她们应聘秘书工作,但只有3个秘书职位,因此5人中仅有三人被录用。如果5人被录用的机会
孩,把她们分别记为A,C,J,K,S。她们应聘秘书工作,但只有3个秘书职位,因此5人中仅有三人被录用。如果5人被录用的机会 均等,分别计算下列事情的概率有多大?
均等,分别计算下列事情的概率有多大?
(1)女孩K得到一个职位
(2)女孩K和S各得到一个职位
(3)女孩K或S得到一个职位
(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量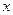 (吨)与相应的生产能耗
(吨)与相应的生产能耗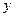 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
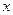 |
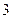 |
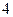 |
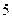 |
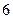 |
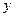 |
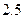 |
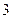 |
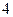 |
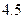 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出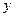 关于
关于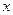 的线性回归方程
的线性回归方程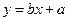 ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:
(参考数值: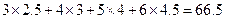 ,
,
(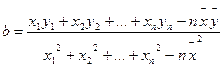 ,
,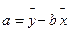 )
)