某观赏鱼池塘中养殖大量的红鲫鱼与金鱼,为了估计池中两种鱼数量情况,养殖人员从池中捕出红鲫鱼和金鱼各1000条,并给每条鱼作上不影响其存活的记号,然后放回池内,经过一段时间后,再从池中随机捕出1000条鱼,分别记录下其中有记号的鱼数目,再放回池中,这样的记录作了10次,将记录数据制成如图所示的茎叶图.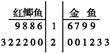
(1)根据茎叶图分别计算有记号的两种鱼的平均数,并估计池塘中两种鱼的数量.
(2)随机从池塘中逐条有放回地捕出3条鱼,求恰好是1条金鱼2条红鲫鱼的概率.
过双曲线
的右焦点
作倾斜角为
的直线交双曲线于A、B两点，
（1）求线段AB的中点C到右焦点的距离。
（2）求线段AB的长。
已知命题
：方程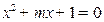
有两个不相等的实根；
：不等式
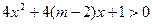的解集为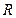
；
若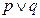
为真，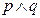
为假，求实数
的取值范围。
分）已知：如图，矩形ABCD，PA⊥平面ABCD, M、N、R分别是AB、PC、CD的中点.
（1）求证：直线MN⊥直线AB ；
（2）若PA=AB=2，AD=1，求直线NR与平面PAR所成角的大小；
（3）若平面PDC与平面ABCD所成的二面角为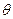
，能否确定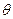使直线MN是异面直线AB与PC的公垂线，若能确定，求出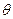的值，若不能确定，说明理由.
 |
如图，在直三棱柱 ABC- A 1 B 1 C 1中，∠ ACB=90°， AC= BC=CC 1=1,
M为 AB的中点,D为BB 1中点. 
（1）求证：平面 CMD⊥平面 ABB 1 A 1；
（2）求点 A 1到平面 CMD的距离. 
．(本小题满分12分)高2011级某班"成长共同体"共有男生3人,女生3人.
（1）6个人站成一排，共有多少种站法？ 
（2）6个人站成一排，女生不相邻，共有多少种站法？
（3）6个人站成一排合影, 女生必须站在一起的排法总数为多少?