已知椭圆C1: +
+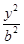 =1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
(1)求椭圆C1的方程;
(2)设点P在抛物线C2:y=x2+h(h∈R)上,C2在点P处的切线与C1交于点M,N.当线段AP的中点与MN的中点的横坐标相等时,求h的最小值.
已知函数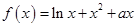 ,
,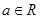 .
.
(1)若函数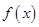 在其定义域上为增函数,求
在其定义域上为增函数,求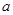 的取值范围;
的取值范围;
(2)当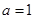 时,函数
时,函数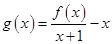 在区间
在区间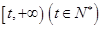 上存在极值,求
上存在极值,求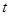 的最大值.
的最大值.
(参考数值:自然对数的底数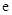 ≈
≈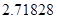 ).
).
已知等差数列 的前
的前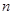 项和为
项和为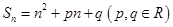 ,且
,且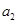 、
、
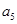 成等比数列.
成等比数列.
(1)求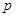 、
、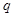 的值;
的值;
(2)若数列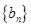 满足
满足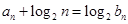 ,求数列
,求数列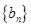 的前
的前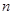 项和
项和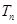 .
.
如图,在五面体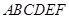 中,四边形
中,四边形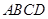 是边长为
是边长为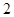 的正方形,
的正方形, 平面
平面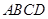 ,
,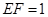 ,
,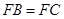 ,
,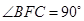 ,
, ,
,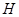 是
是 的中点.
的中点.
(1)求证: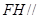 平面
平面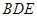 ;
;
(2)求证: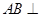 平面
平面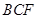 ;
;
(3)求五面体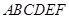 的体积.
的体积.
某校高三年级一次数学考试后,为了解学生的数学学习情况,随机抽取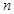 名学生的数学成绩,制成表所示的频率分布表.
名学生的数学成绩,制成表所示的频率分布表.
| 组号 |
分组 |
频数 |
频率 |
| 第一组 |
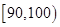 |
 |
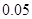 |
| 第二组 |
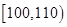 |
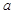 |
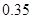 |
| 第三组 |
 |
 |
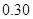 |
| 第四组 |
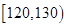 |
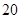 |
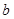 |
| 第五组 |
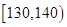 |
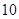 |
 |
| 合计 |
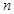 |
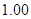 |
(1)求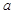 、
、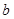 、
、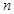 的值;
的值;
(2)若从第三、四、五组中用分层抽样方法抽取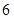 名学生,并在这
名学生,并在这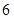 名学生中随机抽取
名学生中随机抽取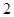 名学生与张老师面谈,求第三组中至少有
名学生与张老师面谈,求第三组中至少有 名学生与张老师面谈的概率
名学生与张老师面谈的概率
已知函数 ,
, .
.
(1)求函数 的最小正周期和值域;
的最小正周期和值域;
(2)若 ,且
,且 ,求
,求 的值.
的值.