为迎接2013年“两会”（全国人大3月5日-3月18日、全国政协3月3日-3月14日）的胜利召开，某机构举办猜奖活动，参与者需先后回答两道选择题，问题A有四个选项，问题B有五个选项，但都只有一个选项是正确的，正确回答问题A可获奖金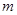
元，正确回答问题B可获奖金
元．活动规定：参与者可任意选择回答问题的顺序，如果第一个问题回答错误，则该参与者猜奖活动中止．假设一个参与者在回答问题前，对这两个问题都很陌生，试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大．
（本小题满分16分）
已知函数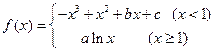
的图象过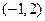点
，且在点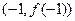
处的切线与直线
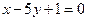垂直．
(1) 求实数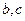
的值；(6分)
(2) 求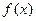
在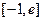
（
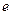为自然对数的底数）上的最大值；(5分)
(3) 对任意给定的正实数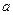
，曲线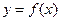
上是否存在两点
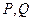，使得
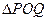是以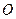
为直角顶点的直角三角形，且此三角形斜边中点在
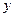轴上？(5分)
（本小题满分16分）
两县城A和B相距20km，现计划在两县城外以AB为直径的半圆弧
上选择一点C建造垃圾处理厂，其对城市的影响度与所选地点到城市的的距离有关，对城A和城B的总影响度为城A与城B的影响度之和，记C点到城A的距离为x km，建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为k ,当垃圾处理厂建在的中点时，对城A和城B的总影响度为0.065.
（1）按下列要求建立函数关系式：
（i）设
（rad），将
表示成
的函数；并写出函数的定义域. (5分)
（ii）设
（km），将表示成
的函数；并写出函数的定义域.(5分)
（2）请你选用（1）中的一个函数关系确定垃圾处理厂的位置，使建在此处的垃圾处理厂对城A和城B的总影响度最小？(6分)
(本题满分15分)
已知数列{an}的前n项和为Sn，且a1=1，Sn=n2an（n∈N*）.
（1）试求出S1，S2，S3，S4，并猜想Sn的表达式；
（2）用数学纳法证明你的猜想，并求出an的表达式.
(本题满分15分)
已知a、b∈（0，+∞），且a+b=1,
求证：(1) ab≤
(2)
+
≥8; (3) 
+ 
≥
. (5分+5分+5分)
（本小题满分14分）
已知
p：
，q：
．
⑴ 若p是q充分不必要条件，求实数
的取值范围；
⑵若“非p”是“非q”的充分不必要条件，求实数的取值范围．