甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面,不同的安排方法共有多少种?
在数列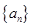 中,
中, .从数列
.从数列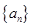 中选出
中选出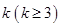 项并按原顺序组成的新数列记为
项并按原顺序组成的新数列记为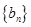 ,并称
,并称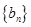 为数列
为数列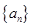 的
的 项子列.例如数列
项子列.例如数列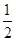 、
、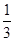 、
、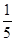 、
、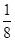 为
为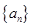 的一个
的一个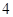 项子列.
项子列.
(1)试写出数列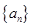 的一个
的一个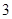 项子列,并使其为等差数列;
项子列,并使其为等差数列;
(2)如果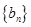 为数列
为数列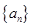 的一个
的一个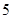 项子列,且
项子列,且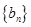 为等差数列,证明:
为等差数列,证明: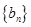 的公差
的公差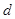 满足
满足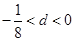 ;
;
(3)如果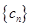 为数列
为数列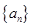 的一个
的一个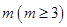 项子列,且
项子列,且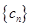 为等比数列,证明:
为等比数列,证明:
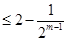 .
.
已知椭圆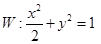 ,直线
,直线 与
与 相交于
相交于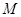 、
、 两点,
两点, 与
与 轴、
轴、 轴分别相交于
轴分别相交于 、
、 两点,
两点,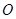 为坐标原点.
为坐标原点.
(1)若直线 的方程为
的方程为 ,求
,求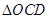 外接圆的方程;
外接圆的方程;
(2)判断是否存在直线 ,使得
,使得 、
、 是线段
是线段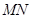 的两个三等分点,若存在,求出直线
的两个三等分点,若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知函数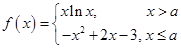 ,其中
,其中 .
.
(1)当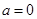 时,求函数
时,求函数 的图象在点
的图象在点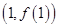 处的切线方程;
处的切线方程;
(2)如果对于任意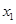 、
、 ,且
,且 ,都有
,都有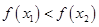 ,求
,求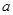 的取值范围.
的取值范围.
如下图,在四棱柱 中,底面
中,底面 和侧面
和侧面 都
都
是矩形,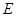 是
是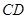 的中点,
的中点, ,
,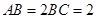 .
.
(1)求证: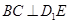
(2)求证: 平面
平面 ;
;
(3)若平面 与平面
与平面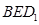 所成的锐二面角的大小为
所成的锐二面角的大小为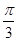 ,求线段
,求线段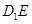 的长度.
的长度.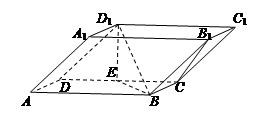

在某批次的某种灯泡中,随机地抽取 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于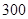 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
| 寿命(天) |
频数 |
频率 |
 |
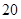 |
 |
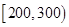 |
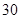 |
 |
 |
 |
 |
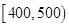 |
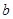 |
 |
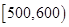 |
 |
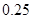 |
| 合计 |
 |
 |
(1)根据频率分布表中的数据,写出 、
、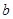 的值;
的值;
(2)某人从灯泡样品中随机地购买了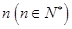 个,如果这
个,如果这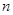 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求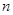 的最小值;
的最小值;
(3)某人从这个批次的灯泡中随机地购买了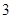 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求 的分布列和数学期望.
的分布列和数学期望.