某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
| 组别 |
分组 |
频数 |
频率 |
| 第1组 |
[50,60) |
8 |
0 16 |
| 第2组 |
[60,70) |
a |
▓ |
| 第3组 |
[70,80) |
20 |
0 40 |
| 第4组 |
[80,90) |
▓ |
0 08 |
| 第5组 |
[90,100] |
2 |
b |
| |
合计 |
▓ |
▓ |

(1)求出 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动
(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;
(ⅱ)求所抽取的2名同学来自同一组的概率
(本小题满分10分)选修4-4:坐标系与参数方程
已知在平面直角坐标系 内,点
内,点 在曲线C:
在曲线C: 为参数,
为参数, )上运动.以
)上运动.以 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)写出曲线C的标准方程和直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线 与曲线C相交于A、B两点,点M在曲线C上移动,试求
与曲线C相交于A、B两点,点M在曲线C上移动,试求 面积的
面积的
最大值.
(本小题满分10分)选修4-1:几何证明选讲
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
(1)求证: ;
;
(2)若 ,试求
,试求 的大小.
的大小.
(本小题满分12分)
若函数f(x)= 在[1,+∞
在[1,+∞ 上为增函数.
上为增函数.
(Ⅰ)求正实数a的取值范围.
(Ⅱ)若a=1,求征:


 (n∈N*且n ≥ 2 )
(n∈N*且n ≥ 2 )
(本小题满分12分)
已知圆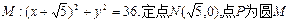 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足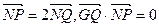 .
.
(I)求点G的轨迹C的方程;
(II)过点(2,0)作直线l,与曲线C交于A、B两点,O是坐标原点,设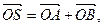 是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
(本小题满分12分)
如图,在直三棱柱 中,
中,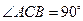 ,
,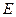 是棱
是棱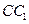 上的动点,
上的动点,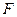 是
是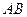 中点,
中点,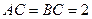 ,
,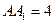 .
.
(Ⅰ)求证: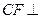 平面
平面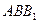 ;
;
(Ⅱ)若二面角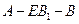 的大小是
的大小是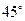 ,求
,求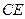 的长.
的长.