(本小题满分10分)选修4-4:坐标系与参数方程
已知在平面直角坐标系 内,点
内,点 在曲线C:
在曲线C: 为参数,
为参数, )上运动.以
)上运动.以 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)写出曲线C的标准方程和直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线 与曲线C相交于A、B两点,点M在曲线C上移动,试求
与曲线C相交于A、B两点,点M在曲线C上移动,试求 面积的
面积的
最大值.
某地有三家工厂,分别位于矩形ABCD 的顶点A,B 及CD的中点P 处,已知AB="20km,CB" ="10km" ,为了处理三家工厂的污水,现要在矩形ABCD 的区域中(含边界),且与A,B等距离的一点O 处建造一个污水处理厂,并铺设排污管道AO,BO,OP ,设排污管道的总长为 km.
km.
(Ⅰ)设∠BAO= (rad),将
(rad),将 表示成
表示成 的函数关系式;
的函数关系式;
(Ⅱ)请用(Ⅰ)中的函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短.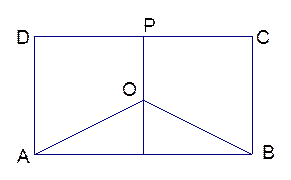
已知数列{ }满足
}满足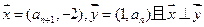 ,
,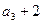 是
是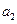 与
与 的等差中项.
的等差中项.
(1)求数列{ }的通项公式
}的通项公式 ;
;
(2)若满足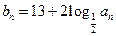 ,
, ,求
,求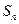 的最大值.
的最大值.
已知向量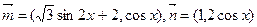 ,设函数
,设函数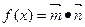 。
。
(1)求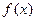 的最小正周期与单调递减区间。
的最小正周期与单调递减区间。
(2)在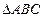 中,
中,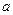 、
、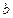 、
、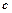 分别是角
分别是角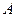 、
、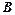 、
、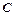
 的对边,若
的对边,若 的面积为
的面积为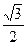 ,求
,求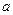 的值
的值
(本小题满分14分)
已知集合 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域内存在
的全体:在定义域内存在 ,使得
,使得 成立。
成立。
(Ⅰ)函数 是否属于集合
是否属于集合 ?说明理由;
?说明理由;
(Ⅱ)设函数 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设函数 图象与函数
图象与函数 的图象有交点,若函数
的图象有交点,若函数 .
.
证明:函数 ∈
∈
(本小题满分12分)
设函数
(I)用五点法画出它在一个周期内的闭区间上的图象;
(II)求函数f(x)的最小正周期及函数f(x)的最大值
(III)求函数f(x)的单调增区间。