在如图的方格纸中，每个小方格都是边长为1个单位的正方形，
的三个顶点都在格点上（每个小方格的顶点叫格点）．
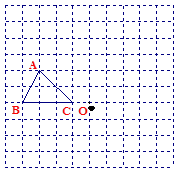
⑴ 画出△ABC关于点O的中心对称的△A1B1C1；
⑵ 如果建立平面直角坐标系，使点B的坐标为（－5，2），点C的坐标为（－2，2），则点A1的坐标为 ；
⑶ 将△ABC绕点O顺时针旋转90°，画出旋转后的△A2B2C2，并求线段BC扫过的面积.
（本题14分）如图，在平面直角坐标系中，点A的坐标为（3，0），直线l与x轴正半轴夹角为30°，点B为直线l上的一个动点，延长AB至点C，使得AB=BC，过点C作CD⊥x轴于点D，交直线l于点F，过点A作AE∥l交直线CD于点E．
（1）若点B的横坐标为6，则点C的坐标为（______，_____），DE的长为；
（2）若点B的横坐标大于3，则线段CF的长度是否发生改变？若不变，请求出线段CF的长度；若改变，请说明理由；
（3）连结BE，在点B的运动过程中，以OB为直径的⊙P与△ABE某一边所在的直线相切，请求出所有满足条件的DE的长．
（本题12分）为迎接中国森博会，某商家计划从厂家采购A，B两种产品共20件，产品的采购单价（元/件）是采购数量（件）的一次函数，下表提供了部分采购数据．
| 采购数量（件） |
1 |
2 |
… |
| A产品单价（元/件） |
1480 |
1460 |
… |
| B产品单价（元/件） |
1290 |
1280 |
… |
（1）设A产品的采购数量为x（件），采购单价为y1（元/件），求y1与x的关系式；
（2）经商家与厂家协商，采购A产品的数量不少于B产品数量的
，且A产品采购单价不低于1200元，求该商家共有几种进货方案；
（3）该商家分别以1760元/件和1700元/件的销售单价售出A，B两种产品，且全部售完，在（2）的条件下，求采购A种产品多少件时总利润最大，并求最大利润．
（本题10分）如图所示,△ABC中,∠BAC=900,AB=AC=1,点D是BC上一个动点（不与B.C重合）,在AC上取点E,使∠ADE=450.
（1）求证:△ABD∽△DEC.
（2）设BD=x,AE=y,求y关于x的函数关系式。
（3当△ADE是等腰三角形时，求AE的长。
（本题10分）已知直线PD垂直平分⊙O的半径OA于点B，PD交⊙O于点C、D，PE是⊙O的切线，E为切点，连结AE，交CD于点F．
（1）若⊙O的半径为8，求CD的长；
（2）证明：PE=PF；
（本题本题10分）如图，在平面直角坐标系中，O是坐标原点，抛物线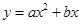
与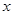
轴正半轴交于点A，对称轴DE交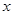轴于点E．点B在第二象限，过点B作BC⊥x轴于点C，连结AB，且AB=10，AC=8．将点B向右平移5个单位后，恰好与抛物线的顶点D重合．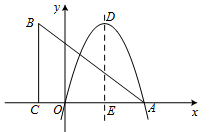
（1）求点D的坐标；
（2）求该抛物线的解析式．