求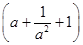 10展开式中的常数项.
10展开式中的常数项.
由0,1,2,3,4,5这六个数字.
(1)能组成多少个无重复数字的四位数?
(2)能组成多少个无重复数字的四位偶数?

(3)能组成多少个无重复数字且被25个整除的四位数?
(4)组成无重复数字的四位数中比4032大的数有多少个?
求出矩阵A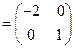 的特征值和特征向量.
的特征值和特征向量.
已知: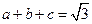 ,求证:
,求证:
(Ⅰ)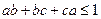 .
.
(Ⅱ)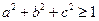 .
.
已知二次函数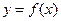 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为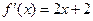 ,数列
,数列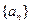 的首项
的首项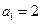 ,点
,点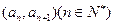 均在函数
均在函数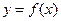 的图象上.
的图象上.
(Ⅰ)求证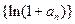 是公比为2的等比数列.
是公比为2的等比数列.
(Ⅱ)记bn=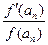 ,求数列
,求数列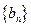 的前项和
的前项和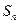 .
.
如图, 是抛物线
是抛物线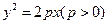 的焦点,过
的焦点,过 轴上的动点
轴上的动点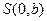 作直线
作直线 的垂线
的垂线 .
.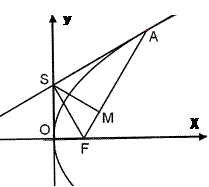
(Ⅰ)求证:直线 与抛物线
与抛物线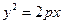 相切;
相切;
(Ⅱ)设直线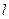 与抛物线
与抛物线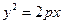 相切于点
相切于点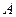 ,过点
,过点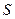 作直线
作直线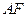 的垂线,垂足为
的垂线,垂足为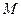 ,求线段
,求线段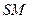 的长度以及动点
的长度以及动点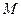 的轨迹方程.
的轨迹方程.