为进一步建设秀美、宜居的生态环境，某村欲购买甲、乙、丙三种树-优题课

为进一步建设秀美、宜居的生态环境，某村欲购买甲、乙、丙三种树美化村庄，已知甲、乙、丙三种树的价格之比为2∶2∶3，甲种树每棵200元，现计划用210 000元资金，购买这三种树共1000棵.
（1）求乙、丙两种树每棵各多少元？
（2）若购买甲种树的棵数是乙种树的2倍，恰好用完计划资金，求这三种树各能购买多少棵？
（3）若又增加了10120元的购树款，在购买总棵数不变的前提下，求丙种树最多可以购买多少棵？

科目数学题型解答题难度中等

知识点：含绝对值的一元一次不等式

为了解七年级学生上学期参加社会实践活动的情况，随机抽查 $A$ 市七年级部分学生参加社会实践活动天数，并根据抽查结果制作了如下不完整的频数分布表和条形统计图．

$A$ 市七年级部分学生参加社会实践活动天数的频数分布表

天数	频数	频率
3	20	0.10
4	30	0.15
5	60	0.30
6	$a$	0.25
7	40	0.20

$A$ 市七年级部分学生参加社会实践活动天数的条形统计图

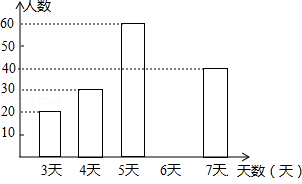
根据以上信息，解答下列问题；

（1）求出频数分布表中 $a$ 的值，并补全条形统计图．

（2） $A$ 市有七年级学生20000人，请你估计该市七年级学生参加社会实践活动不少于5天的人数．

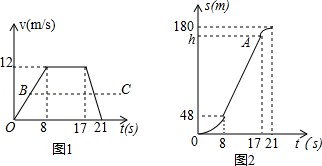
小明的爸爸和妈妈分别驾车从家同时出发去上班，爸爸行驶到甲处时，看到前面路口时红灯，他立即刹车减速并在乙处停车等待，爸爸驾车从家到乙处的过程中，速度 $v (m / s)$ 与时间 $t (s)$ 的关系如图1中的实线所示，行驶路程 $s (m)$ 与时间 $t (s)$ 的关系如图2所示，在加速过程中， $s$ 与 $t$ 满足表达式 $s = a t^{2}$

（1）根据图中的信息，写出小明家到乙处的路程，并求 $a$ 的值；

（2）求图2中 $A$ 点的纵坐标 $h$ ，并说明它的实际意义；

（3）爸爸在乙处等待7秒后绿灯亮起继续前行，为了节约能源，减少刹车，妈妈驾车从家出发的行驶过程中，速度 $v (m / s)$ 与时间 $t (s)$ 的关系如图1中的折线 $O - B - C$ 所示，加速过程中行驶路程 $s (m)$ 与时间 $t (s)$ 的关系也满足 $s = a t^{2}$ ，当她行驶到甲处时，前方的绿灯刚好亮起，求此时妈妈驾车的行驶速度．

我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”

（1）概念理解：

请你根据上述定义举一个等邻角四边形的例子；

（2）问题探究：

如图1，在等邻角四边形 $ABCD$ 中， $∠ DAB = ∠ ABC$ ， $AD$ ， $BC$ 的中垂线恰好交于 $AB$ 边上一点 $P$ ，连接 $AC$ ， $BD$ ，试探究 $AC$ 与 $BD$ 的数量关系，并说明理由；

（3）应用拓展：

如图2，在 $Rt Δ ABC$ 与 $Rt Δ ABD$ 中， $∠ C = ∠ D = 90 °$ ， $BC = BD = 3$ ， $AB = 5$ ，将 $Rt Δ ABD$ 绕着点 $A$ 顺时针旋转角 $α (0 ° < ∠ α < ∠ BAC)$ 得到 $Rt$ △ $AB' D'$ （如图 $3)$ ，当凸四边形 $AD' BC$ 为等邻角四边形时，求出它的面积．

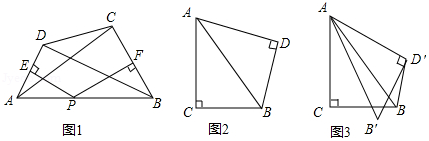
如图1，已知点 $E$ ， $F$ ， $G$ ， $H$ 分别是四边形 $ABCD$ 各边 $AB$ ， $BC$ ， $CD$ ， $DA$ 的中点，根据以下思路可以证明四边形 $EFGH$ 是平行四边形：

（1）如图2，将图1中的点 $C$ 移动至与点 $E$ 重合的位置， $F$ ， $G$ ， $H$ 仍是 $BC$ ， $CD$ ， $DA$ 的中点，求证：四边形 $CFGH$ 是平行四边形；

（2）如图3，在边长为1的小正方形组成的 $5 \times 5$ 网格中，点 $A$ ， $C$ ， $B$ 都在格点上，在格点上画出点 $D$ ，使点 $C$ 与 $BC$ ， $CD$ ， $DA$ 的中点 $F$ ， $G$ ， $H$ 组成正方形 $CFGH$ ；

（3）在（2）条件下求出正方形 $CFGH$ 的边长．

如图，已知一次函数 $y_{1} = kx + b$ 的图象与反比例函数 $y_{2} = \frac{4}{x}$ 的图象交于点 $A (- 4, m)$ ，且与 $y$ 轴交于点 $B$ ，第一象限内点 $C$ 在反比例函数 $y_{2} = \frac{4}{x}$ 的图象上，且以点 $C$ 为圆心的圆与 $x$ 轴， $y$ 轴分别相切于点 $D$ ， $B$

（1）求 $m$ 的值；

（2）求一次函数的表达式；

（3）根据图象，当 $y_{1} < y_{2} < 0$ 时，写出 $x$ 的取值范围．